TU Wien:AKNUM Computernumerik VO (Schranz-Kirlinger)/Katalog potentieller Fragen

Hier ein Katalog möglicher Fragen, Sachen in eckigen Klammern sind TODOs.

Übungsorientiert

Fragen die sich auf Dinge beziehen die so direkt in Übungsbeispielen durchgenommen wurden (also z.B. Fragen die der Übungsleiter den an der Tafel gestellt hat).

Fehlerbetrachtungen

Was sind die absoluten/relativen Fehlerschranken fürs Runden/Abschneiden?

Größter Abstand zwischen zwei benachbarten normalisierten Gleitkomma-Maschinenzahlen:

$\underbrace {(d_{\ell }-(d_{\ell }-1))} _{\text{Differenz benachbarter letzter Stellen}}\cdot b^{-\ell }\cdot b^{e}=b^{e-\ell }$

wobei $b$ die Basis, $\ell$ die Anzahl der Mantissenstellen, und $e$ der Exponent.

Damit ist das die obere absolute Schranke für den Abschneidefehler und die Hälfte davon für den absoluten Rundungsfehler.

Der relativer Fehler [erklären wozu?] ist die der Absolutfehler durch den genauen Wert (falls dieser ungleich 0): ${\tfrac {|{\tilde {x}}-x|}{|x|}}$

Es gilt somit:

• der Zähler ist der absolute Fehler
• der Nenner ist nach unten beschränkt durch $1\cdot b^{-1}\cdot b^{e}=b^{e-1}$, denn die erste Ziffer der Mantisse muss bei einer normalisierten Zahl größer als Null sein.

Nach dem Kürzen fällt der vom Exponentenwert abhängige Teil weg und $b^{1-\ell }$ ist damit eine sinnvolle relative Fehlerobergrenze beim Abschneiden (beim Runden wieder die Hälfte davon). [evtl. relativen Fehler und dessen Relevanz erklären]

Zusammengefasst, Formeln aus dem Skriptum:

$x=(d_{1}\cdot b^{-1}+...)\cdot b^{e}$

Schranke für absoluten Abschneidefehler: $b^{-l}\cdot b^{e}$

Schranke für absoluten Rundungsfehler: ${\frac {1}{2}}b^{-l}\cdot b^{e}$

und

${\tilde {x}}=x(1+\epsilon )$

Schranke für relativen Abschneidefehler: $|\epsilon |<b\cdot b^{-l}$

Schranke für relativen Rundungsfehler: $|\epsilon |\leq {\frac {1}{2}}b\cdot b^{-l}$

Was ist mit "Auslöschung" in der (Computer-)Numerik gemeint?

Auslöschung ist wenn die Subtraktion von zwei annähernd gleich großen Zahlen dazu führt, dass Fehler (z.B. Rundungsfehler in vorigen Berechnungen) noch mehr relevant werden, so dass u.U. ein Ergebnis ungleich 0 erhalten wird, welches nur mehr Fehlerwerte darstellt (→ eine Art schlechte Kondition, da wenn davon ausgegangen wird, dass die hinteren Stellen der Eingangszahlen durch Fehler beeinflusst wurden, diese nun völlig das Ergebnis der Subtraktion ausmachen).

Was ist die Rundungsfehleranalyse? Techniken dazu?

Techniken:

• Statistische Schätzungen der Rundungsfehler
• A-posteriori (Ab)schätzungen: machen keine wirkliche mathematische Aussage über alle denkbaren Anwendungsfälle des untersuchten Algorithmus. In konkreten Fällen unter Einbeziehung des rundungsfehlerbehafteten Resultates führen sie aber zu einer a-posteriori Schätzung des Rundungsfehlers
• Experimentielle Rundungsfehlerschätzungen: Es wird durch künstliche Störungen bei den einzelnen Rechenschritten eines Algorithmus die Rundungsfehlersensitivität der gegebenen Problemdaten experimentiell erprobt
• (1+$\epsilon$)-Technik: wird nur zur Analyse von kleineren Programmstücken eingesetzt

Was beschreibt "Kondition"? Was ist eine gute Kondition? Was sind gut konditionierte Probleme?

• Reaktion auf Datenänderungen ("Empfindlichkeit")
• gute Kondition: höchstens gleich starke Änderung der Lösung
• Schlecht konditionierte Probleme sind wenn die Konditionszahl deutlich größer als 1 ist, sonst sind es gut konditionierte Probleme. Wenn die Konditionszahl unendlich ist, spricht man von einem schlecht gestellten Problem
• Wenn ein Problem schlecht konditioniert ist, kann man es manchmal umformulieren, damit es besser konditioniert ist. Zum Beispiel kann man bei einer Matrix die Zeilen umtauschen, damit sich eine bessere Gesamtkondition ergibt

Welche Konditionszahl entspricht was für einer Kondition?

Da Konditionszahl den Faktor um den sich eine Änderung auswirkt (also verstärkt wird) angibt, werden Werten $\geq 1$ als schlecht konditionierte Probleme angesehen.

Wofür Differenzenquotienten? Arten und deren Unterschiede?

Eignet sich zur Näherung an den Wert einer Ableitung an einer Stelle. Wenn f geschlossen darstellbar ist, so ist auch f' geschlossen darstellbar, also könnte man sich f' mittels Ableitungregeln ausrechnen, aber vor allem bei komplizierteren Funktionen ist die Numerische Differentation oft bequemer (zB Newtonverfahren).

Dabei tritt der Verfahrensfehler auf:

Verfahrensfehler = numerische Näherung - exakte Lösung

Arten von Differenzenquotienten (h... (x1 - x0) ):

- einer der einfachen (Vorwärts-/Rückwärts-, also von wo "angenähert" wird)

Differenzenquotient: $f'(x)\approx {\frac {f(x+h)-f(x)}{h}}$

Verfahrensfehler: ${\frac {f(x+h)-f(x)}{h}}-f'(x)$

- zentraler (Mittelwert aus dem Vorwärts- und Rückwärtsquotienten), Fehler von kleinerem Grad

Differenzenquotient: $f'(x)\approx {\frac {f(x+h)-f(x-h)}{2h}}$

Verfahrensfehler: ${\frac {f(x+h)-f(x-h)}{2h}}-f'(x)$

Parameter zur Definition einer (Gleitkomma-)Maschinenzahl?

• Basis
• Mantissenstellen
• Exponentenminimum
• Exponentenmaximum

(Es kann auch dazwischen unterschieden werden, ob nur normalisierte Zahlen zugelassen werden oder nicht, siehe [1], also dass die führenden Mantissenstellen bei Zahlen allen Zahlen außer 0 immer ungleich 0 sind [richtig? hidden bit?])

Numerische Lösung linearer Gleichungssysteme

[was alles bezieht sich jetzt nur auf quadratisch lin. Gleichungssysteme oder welche mit regulären Koeffizientenmatrix (also solche die quadr. und invertierbar ist) und was nicht?]

Was/Wofür ist die Spaltenpivotsuche?

Davon ausgehend, dass das Gauß-Verfahren durchgeführt wird indem eine Spalte nach der anderen durchgegangen wird und dort immer das Diagonalelement hergenommen wird, um mit diesem die Zeilen unter- bzw. oberhalb zu eliminieren (das s.g. Pivotelement), gilt:

• dieses Element darf nicht 0 sein, weil damit lässt sich nichts eliminieren
• dieses Element sollte möglichst beitragsgroß sein, damit der Algorithmus stabiler ist, sich also kleine Fehler (z.B. durch das Runden) nicht zu sehr auf das Endergebnis auswirken (als wenn durch eine möglicherweise sehr kleine Zahl dividiert wird[?])

Darum wird bei der Spaltenpivotsuche das beitragsgrößte Element in der aktuellen Spalte gesucht und dann die aktuelle Zeile mit der Zeile wo dieses Element sich befindet vertauscht.

Wofür? Weil die Gauß-Elimination selbst bei regulären Matrizen nicht immer durchführbar ist. Die Vertauschung bei der Spaltenpivotsuche stellt sicher, dass die Gauß-Elimination bei regulären Matrizen wohldefiniert ist.

Wann ist ein lin. Glg.-System mit einer quadr. Koeff.-Mat. ($A{\vec {x}}={\vec {b}},A\in \mathbb {R} ^{n\times n},b\in \mathbb {R} ^{n}$) eindeutig lösbar? Wann/wie sonst? Wie vorstellbar?

• kann eindeutig gelöst werden wenn alle Zeilen linear unabhängig (bzw. alle Spalten, denn es gilt immer beides gleich) sind.
• vorstellbar wie $n$ Ebenengleichungen, die Frage der Lösbarkeit hängt damit zusammen wie diese zueinander stehen, auch vom numerischen her eignet sich diese Vorstellung, wenn Ebenen fast parallel sind, so liegt eine schlechte Kondition vor [genauer]
• [wann nicht lösbar, wann mehrere Lsg.]

[unmschreiben] [TODO]

Was für eine Matrix führt bei einem linearen Glg.-System mit einer quadr. Mat. zu einer schlechten Kondition?

Eine die fast singulär ist

Was/wofür ist die LU-Zerlegung?

Basis für eine bessere Computerimplementierung des Gauß'schen Eliminationsverfahrens. Eine (reguläre [notw.?], also quadratische, nichtsinguläre) Matrix wird dabei in zwei Matrizen L und U aufgeteilt deren Produkt (in der Reihenfolge $L\cdot U$) die originale Matrix ergibt. Diese sind dabei Dreiecksmatrizen (also Matrizen wo entweder oberhalb oder unterhalb der Hauptdiagonale alle Elemente 0 sind), wobei bei der ersten die unteren (lower) Elemente nicht unbedingt 0 sind und bei der zweiten die oberen (upper), außerdem sind die Diagonalelemente 1.

In dieser Form und wenn die Umformungsschritte um auf diese Form zu kommen aufgezeichnet wurden... [TODO]

Die Lösung mittels den beiden Matrizen erfolgt dann indem zuerst $L{\vec {y}}=b$ und dann $U{\vec {x}}={\vec {y}}$ gelöst wird, wobei das weil es sich eben um Dreiecksmatrizen handelt mit wenig Aufwand verbunden ist.

Vorteil der LU-Zerlegung?

Ein großer Vorteil für die Praxis ist, dass wenn einmal der aufwendigen Schritt des Aufteilens auf LU-Matrizen durchgeführt wurde, dann das lineare Gleichungsysteme mit dieser Koeffizientenmatrix (also mit diesem $A$ in $A{\vec {x}}={\vec {b}}$) für verschiedene rechte Seiten (also verschiedene $b$s) ohne viel Aufwand gelöst werden kann.

Was für Normen für Vektoren wurden durchgenommen?

• (Betrags-)Summennorm/1-Norm: $\|x\|_{1}=\sum _{i=1}^{n}|x_{i}|$, Beitragssumme der Komponenten eines Vektors (Manhattan-Metrik)
• Maximumsnorm/∞-Norm: $\|x\|_{\infty }=\max _{i=1,\dotsc ,n}|x_{i}|$, betragsgrößten Komponente eines Vektors (Schachbrett-Metrik)
• Euklidische Norm/2-Norm: $\|x\|_{2}={\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}$, natürliche Länge eines Vektors

Was für Normen für Matrizen wurden durchgenommen?

• Spaltensummenform: $\|A\|_{1}$, Betragssumme jeder Spalte und Maximum dieser
• Zeilensummennorm: $\|A\|_{\infty }$, Betragssumme jeder Zeile und Maximum dieser
• Natürliche Matrixnorm: $\|A\|_{2}={\sqrt {max\{\lambda _{1},\lambda _{2}\}}}$, (händisch aufwendige) Berechnung über Eigenwerte

Was beschreibt eine relative vs. absolute Fehlerabschätzung bei linearen Gleichungssystemen?

Wahres System: $A{\vec {x}}={\vec {b}}$

Verfälschtes System: ${\tilde {A}}{\vec {\tilde {x}}}={\vec {\tilde {b}}}$

Abgeschätzt werden müssen also die Auswirkungen der Datenstörungen auf das Ergebnis.

Konditionsabschätzungen bezüglich Störungen von ${\vec {b}}$

• Ungestörtes Problem: $A{\vec {x}}={\vec {b}}$
• Gestörtes Problem: $A{\vec {\tilde {x}}}={\vec {\tilde {b}}}={\vec {b}}+\Delta {\vec {b}}$

Absolute Konditionsabschätzung:

$\|\Delta {\vec {x}}\|=\|{\vec {\tilde {x}}}-{\vec {x}}\|\leq \|A^{-1}\|\|\Delta {\vec {b}}\|$

Relative Konditionsabschätzung:

${\frac {\|\Delta {\vec {x}}\|}{\|{\vec {x}}\|}}\leq {\frac {\|A\|\|A^{-1}\|\|\Delta {\vec {b}}\|}{\|A\|\|{\vec {x}}\|}}\leq \|A\|\|A^{-1}\|{\frac {\|\Delta {\vec {b}}\|}{\|{\vec {b}}\|}}$

Konditionsabschätzungen bezüglich Störungen von $A$

• Ungestörtes Problem: $A{\vec {x}}={\vec {b}}$ ($A$...regulär)
• Gestörtes Problem: ${\tilde {A}}{\vec {\tilde {x}}}=(A+\Delta A){\vec {\tilde {x}}}={\vec {b}}$ (${\tilde {A}}=A+\Delta A$... regulär)

Absolute Konditionsabschätzung:

$\|\Delta {\vec {x}}\|\leq \|A^{-1}\|\|{\vec {\tilde {x}}}\|\|\Delta A\|$

Relative Konditionsabschätzung:

${\frac {\|\Delta {\vec {x}}\|}{\|{\vec {\tilde {x}}}\|}}\leq \|A\|\|A^{-1}\|{\frac {\|\Delta A\|}{\|A\|}}$

Berechnung des absoluten und relativen Fehlers laut einer Norm (bei lin. Glg.-Sys.)?

• absoluter Fehlerwert: Norm der Differenz von Resultat und exaktem Wert
• relativer Fehlerwert: absoluter Fehlerwert durch den exakten Wert (wenn dieser ungleich 0)

Berechnung der Konditionszahl für Matrizen (für lin. Gleichungssysteme)?

$\kappa (A)=\|A\|\|A^{-1}\|$

Wobei eine Norm zu wählen ist [inwiefern passende?].

[Je größer die Zahl, desto näher der Singularität?]

Nichtlineare Gleichungssysteme

Zwei Verfahren um sich Nullstellen oder Fixpunkten numerisch anzunähern? In welcher Form muss die Gleichung vorliegen? Wann konvergieren sie und wie schnell?

1. (Fixpunkt-)Iterationsverfahren:

Form d. Gleichung: Fixpunktgleichung ${\vec {T}}(x)=x$

Konvergenz: Falls ${\vec {T}}$ eine kontrahierende Abbildung ist, erfolgt Konvergenz, d.h. $\lim _{k\rightarrow \infty }{\vec {T}}({\vec {x}}_{k})={\vec {x}}^{*}$

Geschwindigkeit der Konvergenz: unter gewissen Umständen lässt sich sagen, dass die Konvergenzgeschwindikeit von der Lippschitzkonstante abhängt.

Langsame Konvergenz je näher L an 1 liegt, rasche Konvergenz für 0 < L << 1

[wie schnell normalerweise, welche Konvergenzklasse]

2. Newtonverfahren:

i.d.R. quadratische Konvergenz, in Form um Nullstellen herauszufinden

Vorgangsweise Iterationsverfahren? A-priori-Abschätzungen? Abbruchbedingungen? Wann kommt es zur Divergenz?

• Gleichung in Fixpunktgleichungsform bringen (manchmal auf mehr als eine Art möglich) und linke Seite mit einem Startwert füttern und das Ergebnis wieder usw.

• Abschätzung unter gewissen Umständen möglich (Abbildung, abgeschlossen, beschränkt, konvex [=nicht "nach oben gekrümmt"], kontrahierend auf D, dann kann mit dem Wissen um $x_{0}$, $x_{1}$ und der Lippschitzkonstante jede k-te Näherung abgeschätzt werden). Unter diesen Umständen kann auch eine zuverlässige Abbruchbedingung in Computerarithmetik festgesetzt werden.

Wie sieht es mit der Eindeutigkeit von Fixpunkten aus? Relation zur "Kontraktion"?

Eine Abbildung $D\subseteq \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}$ heißt [gdw.?] kontrahierend auf $D$, falls sie lipschitzstetig mit einer Lipschitzkonstante $L<1$ ist, d.h. es gilt dass Betrag/Norm [beliebiger Norm] der Differenz beliebiger Funktionswerte in diesem Bereich $D$ nicht größer ist das das $L$-fache der Differenz der Stellen, als Formel: $\|{\vec {T}}({\vec {x}}_{1})-{\vec {T}}({\vec {x}}_{2})\|\leq L\|{\vec {x}}_{1}-{\vec {x}}_{2}\|,\forall x_{1},x_{2}\in D$

(bei $\mathbb {R}$ kann es sich jeder auch bis zum gewissen Maße bildlich vorstellen, in einem Koordinationssystem Vergleich der Intervalle des Definitionsbereichs und des Wertebereichs dazugehörigen Bildwerte und nur falls ersteres kleiner ist als das zweite dann steht fest, dass die Diagonale (1. Winkelhalbierende, deren Schnittpunkte die Fixpunkte sind) nur einmal geschnitten wird.)

Wenn eine solche Abbildung kontraktierend ist und alle ihre Funktionswerte innerhalb des Definitionsbereichs befinden [echte Teilmenge?], dann hat sie genau einen Fixpunkt.

[Stetigkeit?]

Verwendungszweck und Vorgangsweise beim Newtonverfahren? Wann was für Konvergenz und sonst was?

Bei einer stetig differenzierbaren Funktion wird die Tangente an einer Stelle bestimmt und die Nullstelle dieser dient dann als eine Näherung für die Nullstelle der Funktion und kann auch wieder eingesetzt werden um sich weiter anzunähern. Als Folge:

$x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

Der Startwert muss allerdings ausreichend nahe an dem tatsächlichen Punkt sein, also innerhalb eines gewissen Konvergenzbereichs, (und Funktion nicht konstant so dass Ableitung gleich 0 wäre), sonst ist Divergenz oder Oszillation möglich. Falls Konvergez gegeben ist dann ist die Konvergenzordnung allerdings i.d.R. (also z.B. nicht falls mehrfache oder "fast" mehrfache Nullstelle) gleich 2 ([$O(x^{2})$?]).

Abbruchkriterien beim Newtonverfahren?

[Wikipedia]

Mögliche Abbruchkriterien bezüglich einer Restgröße sind:

$\|f(x-n)\|<\epsilon _{1}$ oder $\|x_{n+1}-x_{n}\|<\epsilon _{2}$

Wobei $\epsilon _{1},\epsilon _{2}\in \mathbb {R^{+}}$ die Qualität der Nullstelle bestimmt. In beiden Fällen kann es vorkommen, dass das Abbruchkriterium zu einem „schlechten“ Zeitpunkt erfüllt ist.

Was/wofür ist der Dämpfungsfaktor beim Newton-Verfahren? Funktionsweise?

Beim Newtonverfahren wird immer um einen Wert ${\frac {f(x_{n})}{f'(x_{n})}}$ korrigiert indem dieser bei jedem Folgeglied vom vorigen Wert subtrahiert wird.

Eine Abwandlung des Newtonverfahrens ist eine wo ein Dämpfungsfaktor $\lambda \in (0,1]$ eingeführt wird und dieser auf den Korrekturwert angewendet wird, also: $x_{n+1}=x_{n}-\lambda {\frac {f(x_{n})}{f'(x_{n})}}$.

Dieser Faktor [der nicht kleiner als notwendig sein sollte?] wird dabei bei jedem Schritt evaluiert indem geschaut wird, ob sich dem Nullpunkt angenähert wird oder nicht, also ob gilt, dass der Betrag (bzw. die Norm im $\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}$-Fall mit bestimmten zusätzlichen Bedingungen) des neuen Folgeglieds kleiner ist als der des vorhergehenden, also $|f(x_{i+1})|<|f(x_{i})|$ und falls das nicht zutrifft der Faktor reduziert wird und wieder evaluiert wird usw.

Als Startwert für den Dämpfungsfaktor kann 1 gewählt werden und der Faktor kann reduziert werden indem der Startwert jeweils mit einem nachfolgenden Glied der harmonischen Reihe (${\frac {1}{2}},\;{\frac {1}{3}},\;{\frac {1}{4}},\cdots$) multipliziert wird.

Mit diesem Verfahren lässt sich der Konvergenzbereich des Newton-Verfahrens deutlich vergrößern (falls es einen für eine Funktion gibt).

(Konvergenzeigenschaft wird leicht negativ beeinflusst, wenn dem nicht entgegenwirkt wird und z.B. in dem Bereich wo der Dämpfungsfaktor nichts mehr bringt dieser weggelassen bzw. auf 1 gesetzt wird)

Interpolation und Approximation

Wieviele Stützstellen bräuchte es für ein eindeutige Bestimmung eines Polynoms vom Grad n (Lagrangesche Interpolationsaufgabe)? Wie sieht das naive aber aufwendige Verfahren dazu aus?

• n+1 (verschiedene!)
• Das gesuchte Polynom in Monomform: $c_{0}+c_{1}x+c_{2}x^{2}+\dotsb +c_{n-1}x^{n-1}+c_{n}x^{n}$, daraus lässt sich ein lineares Gleichungssystem mit einer Gleichung je Stützpunkt ableiten wobei die Koeffizienten ($c_{0}$ usw.) die Unbekannten sind, das $x$ die jeweilige Stützstellen repräsentiert und die Stützwerte die jeweilige linke Seite einer Gleichung in dem System ist. In Matrixschreibweise:

$\underbrace {\begin{pmatrix}1&\cdots &x_{0}^{n}\\\vdots &\ddots &\vdots \\1&\cdots &x_{n}^{n}\end{pmatrix}} _{\text{s.g. Vandermondematrix}}{\begin{pmatrix}c_{0}\\\vdots \\c_{n}\end{pmatrix}}={\begin{pmatrix}f(x_{0})\\\vdots \\f(x_{n})\end{pmatrix}}$

Die Lösung von diesem führt zu den Koeffizienten und damit zum Polynom.

Diese Herangehensweise ist für die Praxis zu aufwendig und außerdem kann die Matrix abhängig von den Stützstellen eine schlechte Kondition aufweisen.

Was/wofür ist die Methode der kleinsten Quadrate? Vorgangsweise mittels Gaußschen Normalgleichungen?

Man hat viele Stützpunkte (Messdaten, wobei allerdings davon ausgegangen wird, dass diese mit Fehlern behaftet sind), und will damit die Parameter für ein passendes Polynom finden (dieses allerdings möglichst von einem Grad der kleiner als die Anzahl an Messpunkten ist → Überbestimmung [sonst?]). Es kann als ein Ausgleichsproblem gesehen werden bei dem es darum geht ein zugrundeliegendes Modell herauszufinden (Approximation).

Mittels der Methode der kleinsten Quadrate werden die Parameter jetzt so gewählt, dass die Summe von jeder einzelnen Differenz zum Quadrat von Messpunkt zu Modellwert minimal werden.

Vorteil davon ist, dass wenn die Fehler auf eine bestimmte Art zufällig sind (Erwartungswert gleich 0, unkorreliert, gleiche Varianz) die so berechneten Parameter auch die sind, welche statistisch zu erwarten wären.

Vorgangsweise für Approximation von Polynom von Grad n mittels Normalgleichungssystem

Vandermondematrix basiered auf den m Stützstellen $x_{i}$ erstellen (Spalte je Grad, Zeile je Messwert):

$A={\begin{pmatrix}1&x_{0}&\cdots &x_{0}^{n-1}&x_{0}^{n}\\\vdots &\vdots &\ddots &\vdots &\vdots \\1&x_{m}&\cdots &x_{m}^{n-1}&x_{m}^{n}\end{pmatrix}}$

System von m (Gaußschen) Normalgleichungen aufstellen (im Vektor auf der rechten Seite sind die Messwerte, die verfälschten Funktionswerte), in Matrixform:

$A^{T}A{\begin{pmatrix}c_{0}\\\vdots \\c_{n}\end{pmatrix}}=A^{T}{\begin{pmatrix}y_{0}\\\vdots \\y_{n}\end{pmatrix}}$

Wenn dieses gelöst wird [eindeutig lösbar, falls voller Rang], sind die Koeffizienten für das gesucht Polynom (aufsteigender Grad) das Ergebnis. [gute Kondition von A umso wichtiger, da diese auch quadriert wird]

Was heißt es ein Polynom mittels einer bestimmten Basis auszudrücken und damit eine andere Darstellung zu erhalten? Was für Darstellungen wurden durchgenommen?

Alle reelen Polynomfunktionen bilden einen Vektorraum, dieser kann aufgestellt werden mittels verschiedenen Basen und das erzeugt dann die verschiedenen Darstellungen (Linearkombination von Basisfunktionen):

$p(x)=\sum _{i=0}^{n}\alpha _{i}\varphi _{i}(x)$

Mögliche Basen:

• Monom ($\varphi _{i}(x)=x^{i},\alpha _{i}=c_{i}$)
• Lagrange
• Newton

Was ist die Darstellung eines Polynoms in Lagrange-Basis? Wann mehr/weniger vorteilhaft?

Polynome dargestellt mittels der Lagrange-Basis, es gilt $p(x)=\sum _{i=0}^{n}f(x_{i})\varphi _{i}(x)$ wobei die Basisfunktionen folgendermaßen definiert sind (i = 0, ..., n):

$\varphi _{i}(x)=\prod _{0\leq j\leq n,\,j\neq i}{\frac {x-x_{j}}{x_{i}-x_{j}}}$

Die Basisfunktionen sind also unabhängig von den Stützwerten (diese sind dafür die Skalare der Linearkombination). An dem Verfahren von Vorteil ist also, dass sich zusätzliche Polynome an den gleichen Stützstellen ohne viel Aufwand (also Basisfunktionen müssen nur einmal berechnet werden) interpolieren lassen. Ein Nachteil ist jedoch, dass bei Hinzufügen einer zusätzlichen Stützstelle alles neu berechnet werden muss [in der Praxis schlecht weil dort oft später welche hinzugenommen werden?].

(jede dieser Basisfunktionen hat den Wert 1, wenn an einer Stützstelle für diese Basisfunktion, also gleicher Index, und falls an einer anderen der Stützstellen dann 0)

Wie sieht die Darstellung eines Polynoms in Newton-Form und Berechnung mittels dem Schema der dividierten Differenzen v.a. in der Praxis aus?

Berechnungsmethode für die Gewichte um ein Polynom in der Linearkombination mit Newton-Polynomen darzustellen. Allgemein gilt für ein Polynom als Linearkombination ausgedrückt: $p(x)=\sum _{i=0}^{n}\alpha _{i}\varphi _{i}(x)$.

Die Basisfunktionen sind in diesem Fall hier:

$\varphi _{i}(x)={\begin{cases}0&i=0\\\textstyle \prod _{j=0}^{i-1}\left(x-x_{j}\right)&i>0\end{cases}}$

Und die Skalare (bei Newton-Polynomen "Gewichte" genannt [denn?]) sind die s.g. dividierten Differenzen $\alpha _{i}=f[x_{0},\dotsc ,x_{i}]$ wobei diese rekursiv definiert sind als:

$f[x_{i}]=f_{i}$

$f[x_{i},\dotsc ,x_{j}]={\frac {f[x_{i+1},\dotsc ,x_{j}]-f[x_{i},\dotsc ,x_{j-1}]}{x_{j}-x_{i}}}$

Damit kann das Polynom aufgestellt werden, zusätzlich kann das in der Form des Horner-Schema geschehen (jedes $x$ wo immer es geht aus "Unterpolynomen" herausheben → verschachtelte Klammerausdrücke, insg. weniger Mult., nur Mult. + Addition, also keine Potenzen), siehe de.wikipedia:Polynominterpolation#Auswertung_des_Polynoms:_Horner-Schema.

(Sonst für nur wenige andere Stellen ist es besser stattdessen das Neville-Schema zu verwenden statt das Polynom überhaupt aufzustellen.)

[umschreiben]

Vorteil der Newton-Darstellung von Interpolationspolynomen?

Der Vorteil an dem Schema der dividierten Differenzen, welches bei der Newton-Interpolation angewendet wird, ist, dass falls zu den vorhandenen Punkten ein weiterer Punkt $x_{n+1}(>x_{n})$ hinzugefügt wird, das vorhandene Schema nur um eine weitere untere Schrägzeile erweitert werden muss.

Anders als bei der Lagrange Interpolation, wo man bei so einem Fall alles neu berechnen muss.

Was ist das Neville-Schema?

Unter der Vorraussetzung, dass alle Stützstellen ungleich sind und aufsteigend sortiert sind, es gilt also $x_{0}<x_{1}<\dots <x_{n}$, lässt sich über den Prinzip der dividierten Differenzen folgende Identität herleiten:

$p_{i,j}(x)={\frac {(x-x_{i})p_{i+1,j}(x)-(x-x_{j})p_{i,j-1}}{x_{j}-x_{i}}}$

wobei $i<j$ und sonst $p_{i,i}(x)=f(x_{i})$ ($p_{i,j}(x)$ ist dabei und vom Grad $j-i$ [warum interessant?])

Es ermöglicht es Werte des Newtonschen Interpolationspolynoms direkt zu berechnen. Zur Berechnung eines Wertes an einer bestimmten Stelle ohne das Polynom aufzustellen kann es in der Form eines Dreiecks angeschrieben werden, wobei mit den Stützwerten ganz links begonnen wird, diese in eine Spalte geschrieben werden (die Stellen die $p_{i,i}$-Werte dar) und immer je zwei untereinander benachbarte Werte in der aktuellen Spalte genommen und deren Werte berechnet und rechts davon geschrieben werden ($p_{r,s}$ und $p_{t,u}$ machen also $p_{r,u}$).

Würde jetzt ein weiterer Stützpunkt hinzufügt werden, so reicht es einfach eine Reihe an der unteren Seite des Dreiecks hinzuzufügen (also auszurechnen). Also z.B. der Stützwert $p_{n+1,n+1}$, $p_{n,n}$, $p_{n-1,n+1}$, usw., das ist also ein ganz klarer Vorteil von dem Verfahren.

[Ob ein zusätzlicher Punkt hinzugefügt werden soll, kann durch Vergleich von dem Punkt an der Spitze mit dem links(-oben) davon erfahren werden? Inwiefern?]

[TODO: besser beschreiben]

Was ist das Hermitsche Interpolationspolynom? Besonderheit der Hermiteinterpolation? Wann mehr/weniger vorteilhaft?

• Bei Hermitinterpolation lassen sich auch Ableitungswerte mitberücksichtigen (also Ableitungen eines gewissen Grades, falls die Ableitungswerte vom Grad darunter auch mitnimmt).
• Kann als Erweiterung der Newton-Interpolation nach dem Neville-Schema angesehen werden, die erste Spalte hat Einträge auch für jeden Ableitungswert als ob die Stützstellen mehrfach vorkommen würden, es wird dort allerdings die Formel umdefiniert, davon abgesehen kann wie beim Neville-Schema gerechnet werden.

[TODO: genauer]

Inwiefern ist das Tschebyscheff-Polynom relevant bzgl. Interpolation? Was ist zu beachten?

Runge-Funktion an äquidistanten (blau) und an Tschebyscheff-Stellen (rot) interpoliert

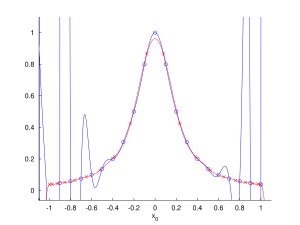
Bei der Polynominterpolation (von z.B. der Funktion von Runge) kann es besser sein die Nullstellen (Abszissen) des Tschebyscheff-Polynom statt äquidistanten Knotenabständen für die Stützstellen zu verwenden. Der Maximalfehler und damit u.U. der Gesamtfehler ist dann kleiner und es wird Probleme an den Rändern bei höheren Graden entgegengesteuert (Runges Phänomen), da sich erstere mit steigendem Grad an den Intervallrändern ansammeln (siehe de.wikipedia:Datei:T30.svg,de.wikipedia:Datei:Interpolation_runge_funktion_10_stuetzstellen.png und das Bild rechts). Die Verteilung der Knoten entspricht dem relativen Fehlerverhalten bei der Approximation.

[Approximiert nicht schlechter als bzgl. der Maximumsnorm bestapproximiertende Polynome]

Zu beachten ist, dass die Nullstellen nur im Bereich $[-1,1]$ existieren, es sind also u.U. Transformationen in diesen Bereich notwendig.

Numerische Integration

Was sind Quadraturformeln? Zwei Beispiele dafür?

• Quadraturformeln sind Formeln zur numerischen Integration einer Funktion auf einem Intervall mittels Polynomen vom Grad $n$, bei Trapezregel werden also einfach Trapeze eingefügt.
• Bei Newton-Cotes-Formeln wird mit äquidistanten Stützstellen gearbeitet. Die Gauß-Quadratur ist ein Beispiel dafür, wenn nicht mit äquidistanten Stellen gearbeitet wird.

Was sind die Newton-Cotes-Formeln?

• Quadraturformeln, also Formeln zur numerischen Integration, wobei bei dieser hier versucht wird das Integral durch eine Polynom zu approximieren und die Stützstellen äquidistant verteilt sind.

• Bei einer Newton-Cotes-Formeln wird approximiert indem Polynome vom Grad $n$ stückweise eingesetzt werden. Dafür wird die Funktion an n+1 Stellen ausgewertet und gewichtet aufsummiert. Die Gewichte sind hierbei spezifisch für jedes n und symmetrisch, d.h. $w_{i}=w_{1-i}$.

$\int _{a}^{b}f(x)\,\mathrm {d} x\approx (b-a)\sum _{i=0}^{n}w_{i}f(x_{i})$

[Intervalmitte, geschlossen/offen?]

Namen der Formeln für $n=1,2{\text{ und }}3$?

Namen:

1. Trapezregel
2. Simpsonregel
3. Pulcherrimaregel (AKA 3/8-Regel)

Konvergenzordnungen

Die Konvergenzordnung, also die Abweichung vom tatsächlichen Integral, ist bei der ersten Formel durch $O(h^{2})$ beschränkt, bei den letzten beiden durch $O(h^{4})$. Ganz allgemein sind höheren Newton-Cotes-Formeln mit ungeraden $n$ insofern nicht besser als mit einer Stelle weniger. [Konvergenzordnung besser erklären, gelten nur für hinreichend glatte Funktionen]

[mit sehr großem $n$ in Praxis auch nicht gut wegen vielen Funktionsauswertungen und wegen Rundungsfehlern und Auslöschung]

Wie können die Newton-Cotes-Formeln hergeleitet werden?

Über Lagrange-Polynome [wie ungefähr?] oder über ein lineares Gleichungssystem.

Beim Gleichungssystem kann mit dem Wissen, dass das Intervall gleichmäßig aufgeteilt wird, schon die Quadraturformel aufgestellt werden (also eigentlich nur gewichtete Summe an Stellen im Intervall im regelmäßigen Abständen) und muss nur noch die Gewichte finden, diese erfährt einer indem ein Gleichungssystem aufstellt wird wo die integrierende Funktion mit verschiedenen Monombasen (die lin. Unabh. ist wichtig!) gleichsetzt wird.

[TODO: besser beschreiben]

Was ist die Simpsonregel?

[Wikipedia]

Die Simpsonregel ist ein Verfahren der numerischen Integration, bei dem eine Näherung zum Integral einer Funktion f(x) im Intervall [a, b] berechnet wird, indem man die schwer zu integrierende Funktion f(x) durch eine exakt integrierbare Parabel P(x) annähert.

Diese Parabel P(x) wird dabei als Interpolationspolynom durch Funktionswerte an den Stellen $a,b,m={\frac {(a+b)}{2}}$ gelegt. Das Integral nähert man dann durch das Integral der Parabel an. Die Simpsonregel ist damit eine sogenannte abgeschlossene Newton-Cotes-Formel.

Was ist die Gauß-Quadratur? Welche bestimmte Form wurde im Detail durchgenommen?

• Stützstellen werden im Ggs. zu den Newton-Cotes-Formeln nicht äquidistant gewählt, sondern optimalerweise an den Nullstellen von Polynomen die ein Orthogonalsystem bilden (d.h. die Polynome sind alle linear unabhängig zueinander). Das Integral wird approximiert durch eine gewichtete Summe, also bei n Knoten $\sum _{i=1}^{n}\Phi (x_{i})w_{i}$, wobei $w_{i}$ die Gewichte sind und $\Phi (x_{i})$ die Werte an den durch das Polygon bestimmten Stellen [beides immer symmetrisch? Also wie als ob von einer geraden Funktion kommend?].

• Man braucht für ein bestimmtes n (Knotenanzahl, von dem die Approximatonsgenauigkeit abhängt) nur einmal die Stützstellen und die Gewichte berechnen und kann es dann für verschiedene numerische Integrationen verwenden.

• im Detail durchgenommen wurde die Verwendung der Nullstellen des Legendre-Polynoms, ein rekursiv definiertes Polynom, bei ungeradem n (Knotenanzahl) ist also der mittlere Knoten 0 [irgendwelche Alleinstellungsmerkmale?], im Bereich $[-1,1]$, für andere Integrationsgrenzen muss zuerst in diesen Bereich verschoben/skaliert werden.

Vorlesungsorientiert

Hier die Sachen hin die ausschließlich in der Vorlesung und nicht in Übungsbeispielen durchgenommen wurden, für die Leute welche die VU machen sind diese wahrscheinlich weniger relevant.

Fehlerbetrachtungen

Was für Fehlerarten gibt es?

• Modellfehler
• Datenfehler
• Verfahrensfehler
• Rechenfehler (Rundungsfehler)

Grund für Modellfehler?

• Modell nicht fein genug (z.B. Elastizität ignorieren)
• (u.U. als Datenfehler …)

Was ist Verfahrensfehler?

Fehler von Näherungen (u.U. weil genaue Berechnung nicht möglich), also Abweichung von genauer Lösung

Unterschiede zwischen Abschätzung in der Arten a-priori und a-posteriori?

• Bei einem Näherungsverfahrenkann im Voraus (a-priori) eine Abschätzung über den möglichen Fehler getroffen werden, z.B. indem Fehlerschranken aufgestellt werden.

• Wenn erst im Nachhinein (a-posteriori) dann die Erkenntnisse des Rechenverlaufs verwenden um eine den Verfahrensfehler abzuschätzen um z.B. zu schauen, ob innerhalb einer gewissen Toleranz.

Numerische Lösung linearer Gleichungssysteme

Was ist die numerische Stabilität eines Algorithmus?

In der numerischen Mathematik heißt ein Verfahren stabil, wenn es gegenüber kleinen Störungen der Daten unempfindlich ist. Insbesondere bedeutet dies, dass sich Rundungsfehler nicht zu stark auf die Berechnung auswirken.

Interpolation und Approximation

Worin besteht der Unterschied zwischen Interpolation und Approximation?

Interpolation:

• Kurve geht durch die exakten eindeutigen Datenpunkte
• Polynominterpolation nur für wenige Punkte sinnvoll
• für große Anzahl von Datenpunkte z.B. Splines verwenden

Approximation:

• Ausgleichsrechnung
• Kurve approximierter Daten
• wenn Daten fehlerhaft
• sehr ungenaue Annäherung → Information zu den Datenpunkten nicht exakt

Numerische Integration

Was ist das Problem bei der Approximation Mehrdimensionaler Integrale?

Aufwand steigt bei Gauß usw. um einiges an, darum wird da eher zu randomisierten Ansätzen übergegangen.

Materialien

Neues Material hinzufügen

T

• tscheb.svg (details)