TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 113
Stellen Sie die folgenden Relationen im kartesischen Koordinatensystem und auch als gerichteten Graphen dar, und untersuchen Sie weiters, ob eine Äquivalenzrelation vorliegt.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
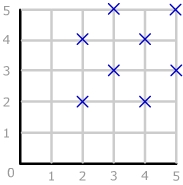
Darstellung im kartesischen Koordinatensystem:
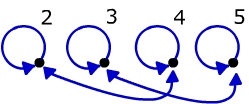
Darstellung anhand von gerichteten Graphen:
(R) - Reflexiv: Ja, da wie am Graphen schön ersichtlich aRa (sprich: jedes a steht in Relation zu a) (S) - Symmetrisch: Ja, da wie ebenfalls am Graphen schön ersichtlich aRb => bRa gilt! (T) - Transitiv: Ja, da aRb und bRc => aRc (die angegebene Menge {2,3,4,5} geht zwar nur bis 5, daher kann man eine Verdeutlichung durch ein Beispiel wie 2R4 u. 4R6 => 2R6 hier nicht bilden. Allerdings geht es ja darum zu bestimmen ob die Relation (T) ist oder nicht!)
Bemerkung zu Transitiv: ist nicht gegeben! a, b und c müssen aus der betrachteten Menge sein!
Edit: Ich denke, es ist doch transitiv, da bei der Transitivität aRb und bRc gelten müssen, woraus dann aRc folgt. Und die wenn die Prämisse, in dem Fall aRb und bRc gilt, dann gilt auch aRc. Deshalb ist die Relation transitiv und folglich eine Äquivalenzrelation.
Lösung laut Tutor CM (2021)[Bearbeiten | Quelltext bearbeiten]
Transitiv: JA - Weil sie auch zu sich selbst in Relation stehen.