TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 114
Stellen Sie die folgende Relation im kartesischen Koordinatensystem und auch als gerichteten Graphen dar, und untersuchen Sie weiters, ob eine Äquivalenzrelation vorliegt.
m R n m - n ungerade oder m = n; m,n {1,2,3,4,5,6}.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Äquivalenzrelation[Bearbeiten | Quelltext bearbeiten]
Eine binäre Relation R auf einer Menge A heißt Äquivalenzrelation, wenn folgende drei Eigenschaften erfüllt sind:
Reflexivität: ,
Symmetrie: ,
Transitivität: .
Ermittlung der Lösungsmenge[Bearbeiten | Quelltext bearbeiten]
- Untersuche alle m = n
{(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}
- Untersuche alle m - n ungerade
{{1, 2}, {1, 4}, {1, 6}, {2, 1}, {2, 3}, {2, 5}, {3, 2}, {3, 4}, {3, 6}, {4, 1}, {4, 3}, {4, 5}, {5, 2}, {5, 4}, {5, 6}, {6, 1}, {6, 3}, {6, 5}}
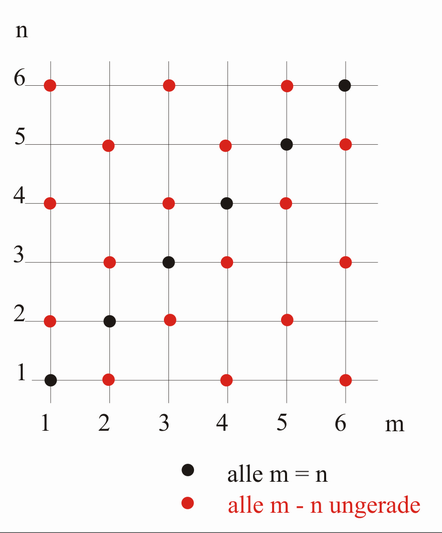
Kartesisches Koordinatensystem[Bearbeiten | Quelltext bearbeiten]
korrigiert --Mnemetz 20:39, 15. Nov 2005 (CET)
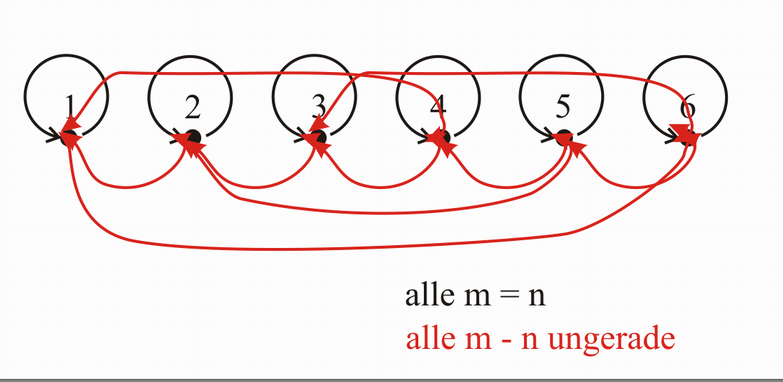
Gerichteter Graph[Bearbeiten | Quelltext bearbeiten]
korrigiert --Mnemetz 20:39, 15. Nov 2005 (CET)
Äquivalenzrelation vorliegend?[Bearbeiten | Quelltext bearbeiten]
Untersuchen wir, ob Reflexivität, Symmetrie und Transitivität gemeinsam vorliegen.
Reflexivität[Bearbeiten | Quelltext bearbeiten]
Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:
Ja, da m = n und {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}.
Geht sehr schön aus dem gerichteten Graphen hervor!
Symmetrisch[Bearbeiten | Quelltext bearbeiten]
Symmetrie heißt, wenn für alle a,b mit aRb auch bRa folgt.
Ja, stimmt.
Die Relation gilt für alle Werte wo m und n gleich sind (hierbei ist es auf jedenfall symetrisch) und wo m - n eine ungerade Zahl ist. Damit m - n ungerade ist muss entweder m gerade und n ungerade oder m ungerade und n gerade sein.
Daher ist die Relation symetrisch da man problemlos einen geraden und dazugehörigen ungeraden Wert tauschen kann, ohne dass die Relation ungültig würde.
Beispiel: (2, 1) befindet sich in der Relation, vertauscht man nun beide Werte so erhält man (1, 2), auch das gehört wieder zu Relation.
(Prof. Gittenberger hat das so erklärt: a - b und b - a unterscheiden sich nur durch einen Vorzeichenwechsel.)
Transitivität[Bearbeiten | Quelltext bearbeiten]
Eine Relation R transitiv, wenn stets gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R
Untersuchen wir:
a b || b c || a c 5 2 || 2 3 || 5 3 Erfüllt nicht!!! 6 1 || 1 4 || 6 4 Erfüllt nicht!!! 6 3 || 3 4 || 6 4 Erfüllt nicht!!!
Somit liegt keine Transitivität vor. Wir haben bereits ein Gegenbeispiel gefunden, welches die Annahme eines Vorliegens der Transitivität in diesem Beispiel ad absurdum führt.
Es liegt somit keine Äquivalenzrelation vor!
Ressourcen[Bearbeiten | Quelltext bearbeiten]
Andere Beispiele[Bearbeiten | Quelltext bearbeiten]
Beispiel 93 Beispiel 100