TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 194
In einer Menge von n Personen können 13 Personen Deutsch, 8 Englisch, 7 Französisch, 5 Deutsch und Englisch, 6 Deutsch und Französisch, 3 Englisch und Französisch, 2 alle drei Sprachen und niemand keine der drei Sprachen. Wie groß ist n?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Siebformel (Ergänzung von mnemetz)[Bearbeiten | Quelltext bearbeiten]
Die Siebformel von Poincaré und Sylvester, auch Formel des Ein- und Ausschließens oder Inklusions-Exklusionsprinzip genannt, dient dazu, die Anzahl der Elemente (Mächtigkeit) einer endlichen Vereinigung nicht-disjunkter Mengen zu berechnen. Sie wird in der Kombinatorik und in der Wahrscheinlichkeitsrechnung verwendet.
Variablen[Bearbeiten | Quelltext bearbeiten]
P ... Menge aller Personen ()
n ... Anzahl der Personen, entspricht der Mächtigkeit von P ()
D ... Menge aller Personen die Deutsch sprechen
E ... Menge aller Personen die Englisch sprechen
F ... Menge aller Personen die Französisch sprechen
Lösungsvorschlag von Soymilk-Drinker[Bearbeiten | Quelltext bearbeiten]
Gesucht ist n also die Mächtigkeit von P. P ist ja wiederum die Vereinigung von D, E und F. Um also auf die Mächtigkeit von P zu kommen verwendet man die Siebformel
Alle einzelnen Komponenten sind durch die Angabe gegeben
(Anzahl der Personen die Deutsch sprechen)
(Anzahl der Personen die Deutsch und Englisch sprechen)
(Anzahl der Personen die alle drei Sprachen sprechen)
Man muss also nur noch in die vorherige Formel einsetzen und erhält die Gesamtanzahl der Personen:
Die gesamte Menge umfasst also 16 Personen
Nachtrag von aläx:
Wäre es nicht einfacher wenn man die Menge aller Personen die Deutsch sprechen und die Menge aller Personen die nicht Deutsch sprechen addiert?
Also
Nachtrag zum Nachtrag von aläx: Diese Überlegung ist falsch, man betrachte dazu nur kurz das VENN-Diagramm und schaue sich "die Menge aller Personen die nicht Deutsch sprechen" an, das ist (im allgemeinen) mehr als und stimmt hier nur zufällig. (Einfach die Rechnung mit anderen Zahlen durchspielen - es stimmt dann nicht mehr.)
Graphische Veranschaulichung (Ergänzung von mnemetz)[Bearbeiten | Quelltext bearbeiten]
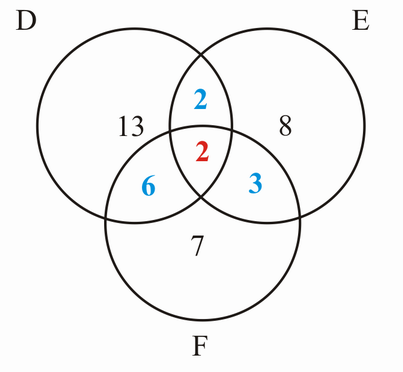
Mit VENN-Diagrammen veranschaulichen wir den Zusammenhang zwischen den Mengen:
Anm. v. PnotNP: Deutsch geschnitten Englisch muss 5 sein, nicht 2.
Siehe auch: Beispiel_160