TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 291
Gegeben sei der ungerichtete Graph mit und . Man veranschauliche G graphisch, bestimme seine Adjazenzmatrix sowie alle Knotengrade und zeige, dass die Anzahl der Knoten, die einen ungeraden Knotengrad besitzen, gerade ist. Gilt diese Aussage für jeden ungerichteten Graphen?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösung[Bearbeiten | Quelltext bearbeiten]
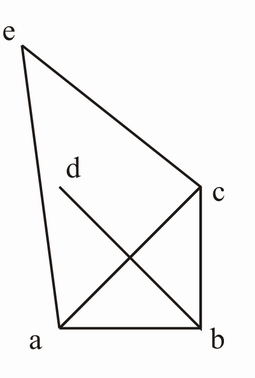
graphische Veranschaulichung (von mnemetz)[Bearbeiten | Quelltext bearbeiten]
Adjazenzmatrix (von ska83)[Bearbeiten | Quelltext bearbeiten]
(berechnet von ska83, in amsmath übertragen von mnmetz)
Knotengrade (von ska83)[Bearbeiten | Quelltext bearbeiten]
d(a) = 3, d(b)= 3, d(c)=3, d(d)=1, d(e)=2
Anzahl der Knoten mit ungeradem Knotengrad (von ska83)[Bearbeiten | Quelltext bearbeiten]
Die Aussage gilt nur dann, wenn es eine gerade Anzahl an ungeraden Knotengraden gibt. Summe d = 2 * |E|
Anzahl der Knoten mit ungeradem Knotengrad (von hanzzz)[Bearbeiten | Quelltext bearbeiten]
Ja die Aussage gilt in jedem ungerichtetem Graphen. (jedenfalls konnte ich kein Gegenbsp. finden ;-) )
Die Summe aller Knotengrade ist ja 2 * |E(G)| (Handschlaglemma) also muss die Summe aller Knotengrade gerade sein.
Die Summe aller Knotengrade muss die Summe aller Knotengrade mit ungeradem Knotengrad + die Summe aller Knotengrade mit geradem Knotengrad sein.
Schauen wir uns mal die Summe aller Knotengrade mit geradem Knotengrad an: Die Summe einer geraden Zahl ist immer gerade. Vgl.: 2 + 4 = 6, 2 + 4 + 6 = 12
Der erste Teil ist also IMMER erfüllt, d.h. die Summe aller Knotengrade mit ungeradem Knotengrad muss auch gerade sein.
Das schauen wir uns mal näher an: Die Summe von ungeraden Zahlen ist nur dann gerade, wenn die Anzahl der Summanden gerade ist. Ist die Anzahl der Summanden ungerade ist die Summe auch ungerade. Dann wäre die Gleichung nicht mehr erfüllt. => Die Anzahl an Knoten mit ungeradem Knotengrad muss gerade sein! Vgl.: 3 + 7 = 10 (Summe von 2 ungerade Zahlen (=gerade Anzahl an Summanden) ergibt immer eine gerade Zahl) 3 + 7 + 5 = 15 (Summe von 3 ungerade Zahlen (=ungerade Anzahl an Summanden) ergibt immer eine ungerade Zahl)
Für diese Ausführung gibts natürlich keine Gewähr. (das ganze stellt man am besten noch mit einer "Gleichung" dar (siehe Weblink) - aber dafür bin ich jetzt zu faul :-P )
Ergänzung von mnemetz[Bearbeiten | Quelltext bearbeiten]
Behauptung Es sei G = {V, E} ein beliebiger ungerichteter Graph. Dann ist die Anzahl der Knoten von G, die einen ungeraden Knotengrad haben, gerade.
Beweis Wir bezeichnen für mit B(v) die Menge der von v ausgehenden Kanten. Da jede Kante von genau zwei Knoten ausgeht, gilt:
Es sei nun U die Menge der Knoten von G mit ungeradem Knotengrad. Dann ist
Umformen liefert:
Nun ist nach Wahl von U |B(v)| fuer alle ungerade und fuer alle gerade. Damit ist auch die Summe ueber alle |B(v)| mit gerade. Also steht auf der rechten Seite der obigen Gleichung eine gerade Zahl, etwa
für ein passendes .
Da die Summanden der Summe auf der linken Seite aber alle ungerade sind, muss ihre Anzahl gerade sein. Die Anzahl der Summanden ist aber gerade |U| = die Anzahl der Knoten von G mit ungeradem Grad. Damit ist die Behauptung gezeigt.
Anzahl der Knoten mit ungeradem Knotengrad (von Soymilk-drinker)[Bearbeiten | Quelltext bearbeiten]
Meine Lösung ist ähnlich der vollständigen Induktion (wenn's nicht sogar ist). Ich suche mir einen Grundzustand der gültig ist und sehe nach ob ich durch Erweiterung auf alle anderen Zustände kommen kann.
Als Grundzustand wähle ich einfach einen Graphen ohne Kanten. Daher haben alle Knoten den Grad 0, und die Anzahl der Knoten mit ungeradem Grad ist somit 0. 0 ist eine gerade Zahl, also stimmt die Behauptung.
Jetzt erweitere ich den Graphen um eine Kante, dabei gibt es 3 Möglichkeiten:
1.) Eine neue Kante wird zwischen 2 Knoten eingefügt die jeweils einen geraden Grad haben. Dadurch erhöht sich der Grad jedes Knoten um 1 und aus gerade wird ungerade. Jetzt haben wir also 2 weitere Knoten mit ungeradem Grad.
2.) Eine neue Kante wird zwischen 2 Knoten eingefügt die jeweils einen ungeraden Grad haben. Dadurch erhöht sich der Grad jedes Knoten um 1 und aus ungerade wird gerade. Jetzt haben wir also 2 weniger Knoten mit ungeradem Grad.
3.) Eine neue Kante wird zwischen 2 Knoten eingefügt wobei ein Knoten einen ungeraden und die andere einen geraden Grad hat. Damit erhöht sich der Grade jedes Knoten um 1, aus dem geraden wird ein ungerader Grad und aus dem ungeraden ein gerader. Damit haben wir einen Knoten mit ungeradem Grad mehr, aber gleichzeitig auch wieder einen weniger (hebt sich also auf)
Ich hab also einen gültigen Anfangszustand (Graph ohne Kanten) und durch hinzufügen von Kanten (3 Fälle) bleibt die Behauptung gültig. Damit ist bewiesen dass die Aussage stimmt.
Hinweis: 2. und 3. können erst auftreten wenn der Graph mindestens eine Kante hat, ansonsten gibts ja nur gerade Grade. Nur falls der Prof nachfragt.
Anmerkung: Schöner Beweis, aber in der Angabe ist nur von ungerichteten Graphen die Rede. Also gibts noch 1 weiteren Fall zu berücksichtigen, nämlich Schlingen. Die erhöhen den Knotengrad von genau einem Knoten um eins (unintuitiv ich weiß). Also gilt die Aussage nicht in jedem ungerichteten Graphen. (Siehe Adjazenzmatrix des Graphen mit Schlinge im Buch als Bsp für einen Graphen der die Aussage nicht erfüllt) (Andererseits steht im Buch auch, dass bei der Gradberechnung Schlingen doppelt gezählt werden müssen, was für mich im Widerspruch zur im Buch dargestellten Adjazenzmatrix steht, die einen ungeraden Knoten darstellt...)
Lösung mit Hnadschlaglemma (wie mnemetz)[Bearbeiten | Quelltext bearbeiten]
Wir setzten einfach in des Hnadschlaglemma ein Dann einsetzten E(G) = 5