TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 292
Welche der nachstehenden Adjazenzmatrizen stellt einen Baum dar?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag von Friday[Bearbeiten | Quelltext bearbeiten]
-- Friday 01.06.2020 11:22 (CEST)
Es wird zwar nicht explizit erwähnt, dass es sich hierbei um ungerichtete Graphen handelt, jedoch ist ein Baum laut Definition 2.23 ein schlichter ungerichteter Graph der keine Kreise positiver Länge enthält. Somit macht es nur Sinn die Adjazenzmatrizen als ungerichtete Graphen zu behandeln.
Matrix A[Bearbeiten | Quelltext bearbeiten]
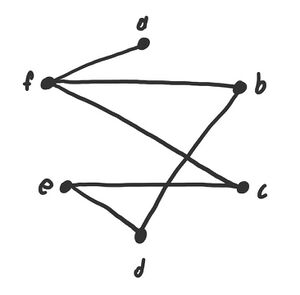
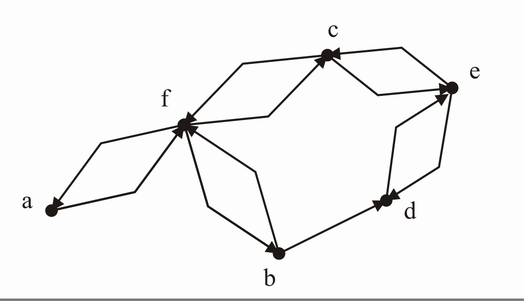
Der Graph ist zwar zusammenhängend, enthält jedoch den Kreis {f, b, d, e, c} und ist somit kein Baum.
Matrix B[Bearbeiten | Quelltext bearbeiten]
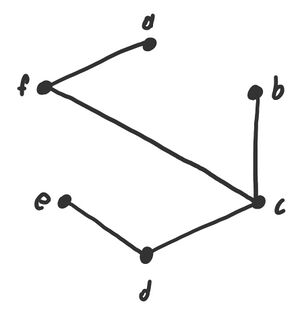
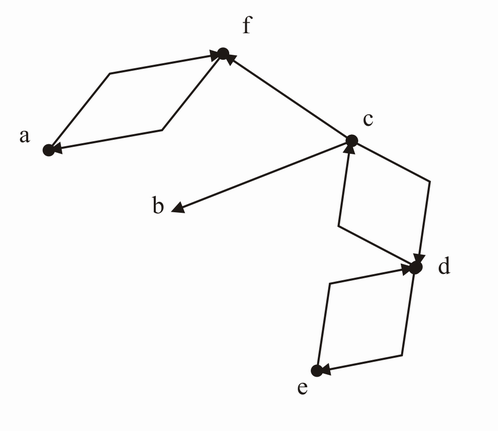
Der Graph ist zusammenhängend und enthält keine Kreise, somit Stellt die Adjezenzmatrix einen Baum da.
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Anmerkung: Die hier dargestellten Graphen enthalten Fehler. Beide Matrizen stellen ungerichtete Graphen da, im Gegensatz zu den hier dargestellten gerichteten Graphen.
Matrix A[Bearbeiten | Quelltext bearbeiten]
Wir müssen überprüfen, ob der durch die Adjazenzmatrix repräsentierte Graph zusammenhängend ist.
Der Graph ist zusammenhängend, jedoch existiert ein Kreis => der vorliegende Graph ist kein Baum!
Anmerkung: Um festzustellen, dass A kein Baum ist, kann man eine spur schneller verfahren, indem man sieht, dass die Anzahl der Kanten = der Anzahl der Knoten ist. Damit ist eine Vorraussetzung für einen Baum verletzt:
Matrix B[Bearbeiten | Quelltext bearbeiten]
Wir müssen überprüfen, ob der durch die Adjazenzmatrix repräsentierte Graph zusammenhängend ist.
Der Graph ist zusammenhängend, also stellt die Adjazenzmatrix einen Baum dar!
edit: - von b geht eine Kante nach c zuruck
- f->c und nicht umgekehrt
anmerkung: für alle, die das auch verwirrend finden: es steht glaub ich nirgends, dass der Graph gerichtet ist, also sind die Kanten von und zu a/f,... eigentlich nur eine ungerichtete Kante. Ansonsten wäre das ja auch schon ein Kreis (bzw. Zyklus)