TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 299
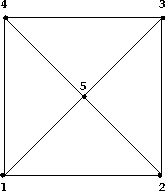
Man bestimme im Graphen mit Hilfe von die Anzahl der Dreiecke (d.h. die Anzahl der Kreise der Länge 3).
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
ist die Adjazenzmatrix von zur dritten Potenz.
Lemma:
Sei ein gerichteter Graph mit Adjazenzmatrix . Dann ist der .Eintrag von gleich der Anzahl der verschiedenen Kantenzüge mit Startknoten i und Endknoten j,welche aus x Kanten bestehen.
Adjazenzmatrix
Kubizierte Adjazenzmatrix:
Wir suchen nach Kreisen im Graphen, d.h. Kantenzüge mit gleichem Start- und Endknoten; das sind genau diejenigen, die die Hauptdiagonale der Adjazenzmatrix bilden.
Man kommt also auf 4 + 4 + 4 + 4 + 8 = 24 Kreise (der Länge 3).
Hier bilden aber etliche Kreise dasselbe Dreieck ab: (abc)=(acb)=(bac)=(bca)=(cab)=(cba), sprich alle Permutationen der drei jeweils beteiligten Knoten.
Um auf die Anzahl der Dreiecke zu kommen, sollte man also die Anzahl der Kreise durch die Anzahl der mögl. Permutationen dividieren:
Dreiecke.
--Baccus 04:14, 7. Dez 2006 (CET)