Man finde alle sechsten Wurzeln von  in
in  und stelle sie in der Gaußschen Zahlenebene dar!
und stelle sie in der Gaußschen Zahlenebene dar!
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Zu lösen ist also: 
Wir müssen die vorliegende Form in die Polarform umwandeln, und zwar in:


 da gilt:
da gilt:


Somit ergibt die Überführung in die Polarform:

Die "Wurzelformel" ist: (Siehe auch http://de.wikibooks.org/wiki/Komplexe_Zahlen#Satz_von_MOIVRE sowie das Beispiel danach auf dieser Website)
Die  entsprechen den
entsprechen den  im folgenden.
im folgenden.
![{\displaystyle z_{0,...,5}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+k*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+k*360^{\circ }}{6}})\qquad k=\{0,1,2,3,4,5\}}](/index.php?title=Spezial:MathShowImage&hash=c364b352f134e20da782a353ef6184a2&mode=mathml)
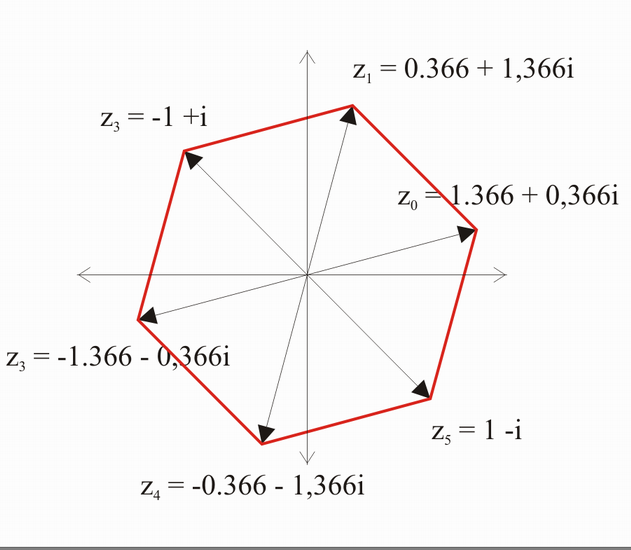
![{\displaystyle k=0\qquad z_{0}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+0*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+0*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(0.9659+i*0.2588)\qquad z_{0}=1.366+0,366i}](/index.php?title=Spezial:MathShowImage&hash=4bfc14fe34ebc9e97d1204e2522ba885&mode=mathml)
![{\displaystyle k=1\qquad z_{1}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+1*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+1*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(0.2588+i*0.9659)\qquad z_{1}=0.366+1,366i}](/index.php?title=Spezial:MathShowImage&hash=16da0352ecbbe7ac94fbf44cb515bf69&mode=mathml)
![{\displaystyle k=2\qquad z_{2}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+2*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+2*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(-0.7071+i*0.7071)\qquad z_{2}=-1+i}](/index.php?title=Spezial:MathShowImage&hash=1f21c186fc53b853444182446f1e08c8&mode=mathml)
![{\displaystyle k=3\qquad z_{3}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+3*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+3*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(-0.9659+i*-0.2588)\qquad z_{3}=-1.366-0,366i}](/index.php?title=Spezial:MathShowImage&hash=d6ec8819c5161433cadec556a77e6d4f&mode=mathml)
![{\displaystyle k=4\qquad z_{4}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+4*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+4*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(-0.2588+i*-0.9659)\qquad z_{4}=-0.366-1,366i}](/index.php?title=Spezial:MathShowImage&hash=83662b741e2330a4b16d54bab822e020&mode=mathml)
![{\displaystyle k=5\qquad z_{5}={\sqrt[{6}]{8}}*(\cos {\frac {90^{\circ }+5*360^{\circ }}{6}}+i\sin {\frac {90^{\circ }+5*360^{\circ }}{6}})={\sqrt[{6}]{8}}*(0.7071+i*-0.7071)\qquad z_{5}=1-i}](/index.php?title=Spezial:MathShowImage&hash=06e6d694c157c8486c85ad39519ef044&mode=mathml)
Siehe auch:
Die Rechnung ist mir viel zu kompliziert, das mit den Winkel geht doch viel einfacher.
Ausgangswinkel / Wurzelgrad = w0
Der Unterschied zwischen den Ergebnissen ist 360 / Wurzelgrad, diesen Abstand braucht man dann nur immer dazu addieren.
w0= 90 / 6 = 15°
Abstand = 360/6 = 60°
w1 = w0+ 60 = 75°
w2 = w1+60 = 135°
w3 = w2+60 = 195°
w4 = w3+60 = 255°
w5 = w4+60 = 315°
Wer unbedingt will kann das auch mit Pi rechnen, dann ists halt Pi/3 das man zu den w0 = Pi/12 hinzuzählen muss.
--Zool 21:58, 12. Nov 2008 (CET)
Wenn man die Angabe in die wirkliche Polarform [Betrag, Winkel] umwandelt, wird das Beispiel sehr einfach (siehe Buch Seite 13,14).
![{\displaystyle z=0+8i=[8,{\frac {\pi }{2}}]}](/index.php?title=Spezial:MathShowImage&hash=74fc11a5948ed467136e0d466f95ecd5&mode=mathml)
![{\displaystyle w={\sqrt[{6}]{8}}(z)}](/index.php?title=Spezial:MathShowImage&hash=7de587fe1188b9d0c89a91e65094db04&mode=mathml)
![{\displaystyle w_{0}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 0}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=f19c00be644f114460221e57d9be519f&mode=mathml)
![{\displaystyle w_{1}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 1}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=fe5dee320b4e74dc020740c3248ed3bc&mode=mathml)
![{\displaystyle w_{2}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 2}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=f8aea18f3e3105a1d54cf7d778ef9ac3&mode=mathml)
![{\displaystyle w_{3}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 3}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=e28c4a83debd7c01564b681e00cba7f2&mode=mathml)
![{\displaystyle w_{4}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 4}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=b94694beed9d9e9661ce9f9b58fb6b60&mode=mathml)
![{\displaystyle w_{5}=[{\sqrt[{6}]{8}},{\frac {\pi }{12}}+{\frac {2\pi \cdot 5}{6}}]}](/index.php?title=Spezial:MathShowImage&hash=0a9d605d8014ccdb00be9f3f3f00c99d&mode=mathml)
--Woife 20:35, 21. Nov 2007 (CET)
