TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 469
Untersuchen Sie, ob Teilraum des Vektorraums über ist und beschreiben Sie die Menge geometrisch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Sei ein Vektorraum, heißt Unterraum oder Teilraum, wenn:
- ist abgeschlossen bezüglich
- ist abgeschlossen bezüglich
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
1. Kriterium[Bearbeiten | Quelltext bearbeiten]
Kriterium 1 des Unterraumkriteriums, , ist erfüllt, da es Vektoren gibt, für die gilt , wie z. B.
2. Kriterium[Bearbeiten | Quelltext bearbeiten]
Das zweite Kriterium ist erfüllt, weil für jede Addition zweier Vektoren aus U gilt, dass die Summe wieder erfüllt: (Abgeschlossenheit bzgl. Addition von ). z. B.
3. Kriterium[Bearbeiten | Quelltext bearbeiten]
Das dritte Kriterium ist erfüllt, weil für jedes Produkt eines Vektors aus U mit einem Skalar aus gilt, dass er wieder die Kondition erfüllt (Abgeschlossenheit bzgl. Multiplikation von ).
z. B.
Es handelt sich bei W also um einen Teilraum des oben genannten Vektorraums.
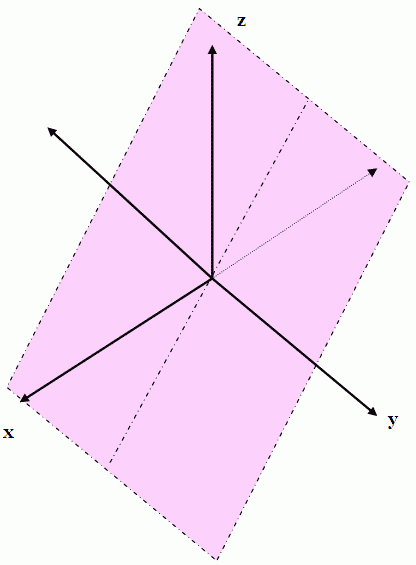
Geometrische Darstellung[Bearbeiten | Quelltext bearbeiten]
Shikantaza 10:15, 30. Mai 2009 (CEST)
Links[Bearbeiten | Quelltext bearbeiten]
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 326
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 327
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 328
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 329
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 330
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 331
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 332
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 333
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 334
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 335