TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 471
Untersuchen Sie, ob Teilraum des Vektorraums über ist und beschreiben Sie die Menge geometrisch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Sei ein Vektorraum, heißt Unterraum oder Teilraum, wenn:
- ist abgeschlossen bezüglich
- ist abgeschlossen bezüglich
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
1. Kriterium[Bearbeiten | Quelltext bearbeiten]
Kriterium 1 des Unterraumkriteriums, , ist erfüllt, da es Vektoren gibt, für die gilt , wie z. B.
2. Kriterium[Bearbeiten | Quelltext bearbeiten]
Es gilt hier die Abgeschlossenheit bzgl. Addition von zu prüfen.
Das zweite Kriterium ist nicht erfüllt, da nicht für jede Addition zweier Vektoren aus U gilt, dass die Summe wieder erfüllt. Wir wählen z. B. die folgenden Vektoren und addieren:
Nun müsste für die Summe der beiden Vektoren gelten . Dies ist jedoch nicht der Fall, weil : Keine Abgeschlossenheit bzgl. Addition lt. Kriterium 2.
3. Kriterium[Bearbeiten | Quelltext bearbeiten]
Das dritte Kriterium ist auch nicht erfüllt, weil für jedes Produkt eines Vektors aus U mit einem Skalar aus gelten müsste, dass es wieder die Kondition erfüllt (Abgeschlossenheit bzgl. Multiplikation von ). Dies ist jedoch auch nicht der Fall.
z. B.
Diese Gleichung stimmt nur für und nicht für alle Werte des Körpers . Somit ist auch das dritte Kriterium nicht erfüllt. Es handelt sich bei W also nicht um einen Teilraum des oben genannten Vektorraums.
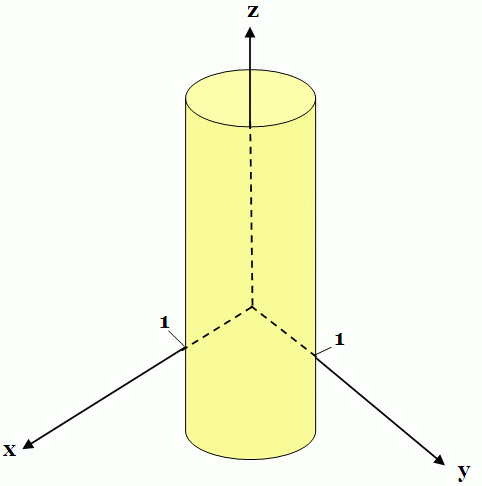
Geometrische Darstellung[Bearbeiten | Quelltext bearbeiten]
Shikantaza 19:24, 30. Mai 2009 (CEST)
Links[Bearbeiten | Quelltext bearbeiten]
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 326
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 327
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 328
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 329
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 330
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 331
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 332
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 333
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 334
- TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 335