TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 507
Sei der Vektorraum aller rellwertigen Funktionen. Untersuchen Sie, ob und mit und linear unabhängig sind.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag von Ryus[Bearbeiten | Quelltext bearbeiten]
Zwei Elemente v1, v2 eines Vektorraums sind genau dann linear unabhängig, wenn gilt (Satz 3.12.):
Der Nullvektor ist also nur durch eine triviale Linearkombination darstellbar.
Um dies in diesem Beispiel zu prüfen, ist nun erstmal zu überlegen, was der Nullvektor in unserem Vektorraum ist. Der Nullvektor dient als neutrales Element der Vektoraddition. Es gilt also für alle : . Die Addition funktioniert dabei so, dass einfach die Formeln der Funktionen addiert werden. (z.B. ). Dies trifft nur auf die Funktion zu. Damit ist diese unser Nullelement.
Nun ist die Frage, ob wir irgendwelche Koeffizienten finden, so dass gilt:
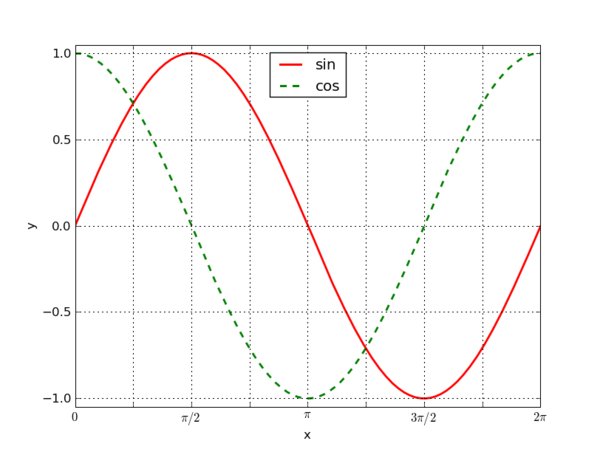
Dazu betrachte man mal eine Sinus- und Cosinus-Kurve:
Durch multiplizieren mit einem Skalar erhöht sich die Amplitude der Kurve und sie wird höher oder niedriger. Damit die beiden Funktionen linear abhängig sind, müssten wir zwei Skalare finden, mit denen wir sie multiplizieren können, so dass ihre Summe die 0-Funktion ergibt. Dies kann jedoch nur der Fall sein, wenn die beiden neuen Kurven gespiegelt verlaufen () oder der 0-Funktion selber entsprechen. Da wir durch Multiplikation mit einem Skalar aber nur die Amplitude verändern können, und nicht etwa die Phase angleichen können (was nötig wäre, damit sie gespiegelt verlaufen), ist die einzige Möglichkeit, die 0-Funktion zu erzeugen, indem wir als Koeffizienten 0 wählen.
Falls das noch nicht ganz klar war, empfehle ich noch, auf den ersten Punkt im Sinus zu achten: (0,0). Durch Multiplikation mit einem Skalar ist dieser sicher nicht änderbar. Damit die Summe von sin+cos an dieser Stelle aber 0 ergibt, muss auch der Cosinus, der eigentlich an dieser Stelle 1 ist, an dieser Stelle 0 werden, und das geht nur, in dem ich ihn mit 0 multipliziere.
Somit gibt es also keine nichttriviale Linearkombination von und die den 0-Vektor darstellt. Somit sind die beiden Funktionen linear unabhängig.