TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 102

Beweisen oder widerlegen Sie die folgenden Identitäten für Mengen:

$(A\times B)\cup (B\times A)=(A\cup B)\times (B\cup A)$

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag von Axel

Beiweise/Wiederlege: $(A\times B)\cup (B\times A)=(A\cup B)\times (A\cup B)$

Sei a Element von A und a kein Element von B. Dann ist wegen a Element von A a auch Element $(A\cup B)$, also (a,a) Element von $(A\cup B)\times (A\cup B)$. Wegen a kein Element B ist aber (a,a) kein Element von $(A\times B)$ und auch kein Element von $(B\times A)$, also auch kein Element von $(A\times B)\cup (B\times A)$.

Damit ist $(A\cup B)\times (A\cup B)$ keine Teilmenge von $(A\times B)\cup (B\times A)$ , womit die Annahme wiederlegt ist.

Lösungsvorschlag von Georg Schiesser

$(A\cup B)\times (A\cup B)=$

$(A\times (A\cup B))\cup (B\times (A\cup B))=$

$(A\times A)\cup (A\times B)\cup (B\times A)\cup (B\times B)$

siehe: http://de.wikipedia.org/wiki/Kartesisches_Produkt

und dann sieht man, dass:

$(A\times A)\cup (B\times B)$

zuviel ist. gilt also nur, wenn:

A = B

Lösungsvorschlag von Johannes

Johannes schlug vor, die Möglichkeiten aufzuzeichnen und so die Identität visuell zu "widerlegen" oder zu "bestätigen".

Seien A = B so ist die Bestätigung trivial.

Seien A und B "nebeneinander" so sieht man:

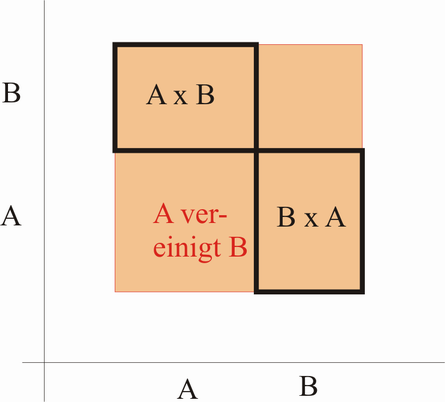
Seien A und B ineinander verschränkt_

Lösungsvorschlag von Jensi

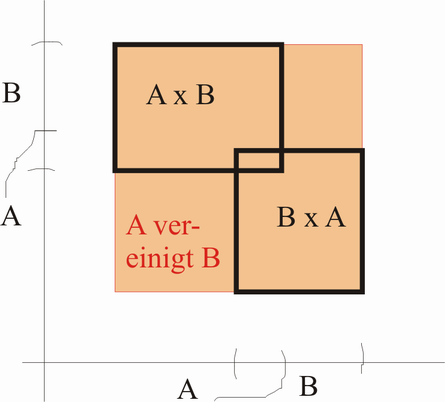
ist umstritten --> Es ist wichtig zu beachten, dass das die geordneten Paare des Kreuzprodukts nicht Kommutativ sind. Die Reihenfolge darf nicht vertauscht werden obwohl das logische "und" schon Kommutativ ist. Daher ist der Beweis falsch.

Die Mengenoperationen $\times$ und $\cup$ sind wie folgt definiert:

$A\times B=\{\langle x,y\rangle \ |\ x\in A\land y\in B\}$

$A\cup B=\{x\ |\ x\in A\lor x\in B\}$

Daher kann man die linke und rechte Seite der Identität folgendermaßen beschreiben:

Linke Seite:

${\begin{array}{rcll}(A\times B)\cup (B\times A)&=&\{z\ |\ z\in (A\times B)\lor z\in (B\times A)\}&|z:=\langle x,y\rangle \\&=&\{\langle x,y\rangle \ |\ \langle x,y\rangle \in (A\times B)\lor \langle x,y\rangle \in (B\times A)\}\\&=&\{\langle x,y\rangle \ |\ (x\in A\land y\in B)\lor (x\in B\land y\in A)\}\end{array}}$

Der Übersichtlichkeit halber definieren wir Terme:

${\begin{array}{rcl}a&:=&x\in A\\b&:=&y\in B\\c&:=&x\in B\\d&:=&y\in A\end{array}}$

So können wir die linke Seite anschreiben als:

$(A\times B)\cup (B\times A)=\{\langle x,y\rangle \ |\ (a\land b)\lor (c\land d)\}$

Rechte Seite:

${\begin{array}{rcl}(A\cup B)\times (A\cup B)&=&\{\langle x,y\rangle \ |\ x\in (A\cup B)\land y\in (A\cup B)\}\\&=&\{\langle x,y\rangle \ |\ (x\in A\lor x\in B)\land (y\in A\lor y\in B)\}\end{array}}$

Wir ersetzen wieder durch die früher definierten Terme a, b, c, d und formen den logischen Ausdruck zwecks besserer Vergleichbarkeit mit der linken Seite durch Ausdistribuieren in die disjunktive Normalform um (der Ausdruck für die linke Seite ist bereits in disjunktiver Normalform):

${\begin{array}{rcl}(A\cup B)\times (A\cup B)&=&\{\langle x,y\rangle \ |\ (a\lor c)\land (d\lor b)\}\\&=&\{\langle x,y\rangle \ |\ (a\land b)\lor (a\land d)\lor (b\land c)\lor (c\land d)\}\end{array}}$

Die Mengen sind nun identisch, wenn die logischen Ausdrücke, die sie definieren, die gleiche Bedeutung haben:

${\begin{array}{rcl}\underbrace {(a\land b)\lor (c\land d)} _{\textrm {linkeSeite}}&=&\underbrace {(a\land b)\lor (a\land d)\lor (b\land c)\lor (c\land d)} _{\textrm {rechteSeite}}\\(a\land b)\lor (c\land d)&=&(a\land b)\lor (c\land d)\lor (a\land d)\lor (c\land b)\qquad (*)\\\end{array}}$

Wir können die Terme etwas umordnen:

$(a\land b)\lor (c\land d)=(a\land b)\lor (c\land d)\lor (a\land d)\lor (c\land b)$

Man sieht, daß die ersten zwei Terme jeder Seite gleich und damit logisch äquivalent sind. Die letzten beiden Terme der rechten Seite unterscheiden sich von den ersten beiden durch die Variablen b und d. Setzen wir nun die Variable d := b, so erhalten wir:

$(a\land b)\lor (c\land b)=(a\land b)\lor (c\land b)\lor (a\land b)\lor (c\land b)$

Da $x\lor x=x$ gilt, gilt auch $(a\land b)\lor (a\land b)=(a\land b)$. Analoges gilt für $(c\land b)$:

$(a\land b)\lor (c\land b)=(a\land b)\lor (c\land b)$

Das bedeutet, daß (*) genau dann gilt, wenn b = d. Sehen wir uns die Definition der Terme an:

${\begin{array}{rcl}b&=&d\\y\in B&=&y\in A\end{array}}$

Die letzte Beziehung gilt genau dann für alle y aus A und B, wenn A = B:

Wenn $y\in B\Rightarrow y\in A\ \forall y\in B$ gilt, so gilt $B\subseteq A$. Auch umgekehrt muß aufgrund der Symmetrie $y\in A\Rightarrow y\in B\ \forall y\in A$ und damit $A\subseteq B$ gelten. Aus $A\subseteq B\land B\subseteq A$ folgt A = B.

(Warnung: Ich bin selbst nicht 100%ig überzeugt von diesem Beweis. Intuitiv muß das gelten, aber formal finde ich das nicht ganz sauber.)

Beispiel

Nehmen wir als Beispiel die Grundmengen $A=\{1\}$ und $B=\{a,b\}$:

$(A\times B)\cup (B\times A)=\{\langle 1,a\rangle ,\langle 1,b\rangle \}\ \cup \ \{\langle a,1\rangle ,\langle b,1\rangle \}=\{\langle 1,a\rangle ,\langle 1,b\rangle ,\langle a,1\rangle ,\langle b,1\rangle \}$

$(A\cup B)\times (A\cup B)=\{\{1,a,b\}\times \{1,a,b\}\}=\{\langle 1,1\rangle ,\langle 1,a\rangle ,\langle 1,b\rangle ,\langle a,1\rangle ,\langle a,a\rangle ,\langle a,b\rangle ,\langle b,1\rangle ,\langle b,a\rangle ,\langle b,b\rangle \}$

Ein weiteres Beispiel für den Fall $A=B=\{a,b\}$:

$(A\times A)\cup (A\times A)=A\times A=\{\langle a,a\rangle ,\langle a,b\rangle ,\langle b,a\rangle ,\langle b,b\rangle \}$

$(A\cup A)\times (A\cup A)=A\times A=\{\langle a,a\rangle ,\langle a,b\rangle ,\langle b,a\rangle ,\langle b,b\rangle \}$