TU Wien:Algorithmen und Datenstrukturen 1 VU (Raidl)/Übungen SS09/Beispiel 16
Bei einer In-Order-Traversierung eines gegebenen binären Baumes ergibt sich folgende Knotenliste:
0, 1, 2, 3, 7, 6, 8, 10, 11, 15, 20, 25
Bei einer Pre-Order-Traversierung des gleichen Baumes ergibt sich:
8, 3, 1, 0, 2, 7, 6, 11, 10, 20, 15, 25
Zeichnen Sie den zugrundeliegendenBaum und tragen Sie die entsprechenden Knotenwerte ein.
Lösung[Bearbeiten | Quelltext bearbeiten]
Es gibt zwar einen binären Baum, der diese Werte erfüllt, allerdings hat dieser ein ungültiges Element!
Hinweis:
- Bei der In-Order-Traversierung wird zuerst der linke Teilbaum aufgebraucht, dann die Wurzel, und dann der rechte Teilbaum.
- Bei der Pre-Order-Traversierung wird zuerst die Wurzel, dann der linke Teilbaum und dann der rechte Teilbaum aufgebraucht.
Herangehensweise[Bearbeiten | Quelltext bearbeiten]
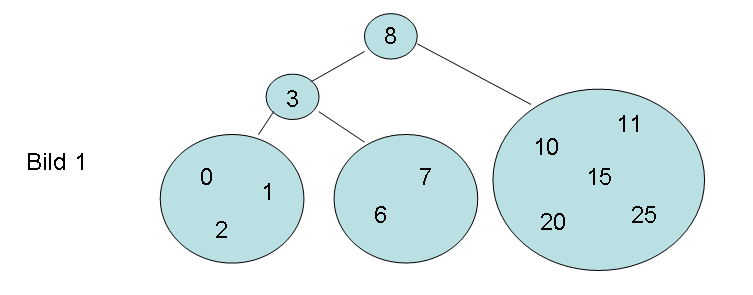
Da in der Pre-Order-Traversierung W,L,R - aufgebraucht wird, muss das erste Element (die 8) die Wurzel sein, und das zweite (die 3) die Wurzel des linken Teilbaums sein (siehe Bild1). Wenn man nun die In-Order-Traversierung (L,W,R) betrachtet, müssen die Elemente davor im linken Teilbaum, die dannach im rechten Teilbaum sein.
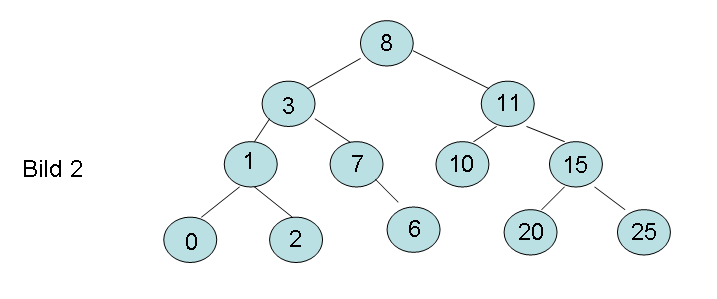
Der fertige Baum sieht dann folgendermaßen aus:
beachte, da es kein Suchbaum ist, gibt es keine Bedingung, dass das rechte Kind größer und das linke Kind kleiner als der Vater sein muss!!