TU Wien:Algorithmen und Datenstrukturen 1 VU (Raidl)/Übungen SS09/Beispiel 29
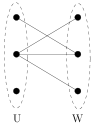
Ein ungerichteter Graph G = (V, E) heißt bipartit, wenn man die Menge V in zwei disjunkte Untermengen U und W so aufspalten kann, dass für alle Kanten gilt: .
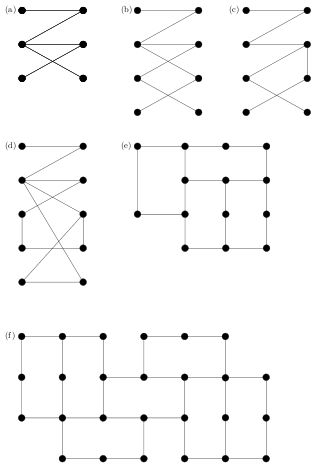
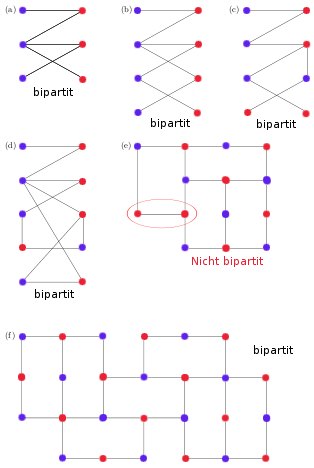
Untersuchen Sie, ob die untenstehenden Graphen bipartit sind und markieren Sie gegebenenfalls die Kanten, die diese Eienschaft verletzen. Erläutern Sie Ihre Vorgehensweise!
Vorgehensweise[Bearbeiten | Quelltext bearbeiten]
Generelle Vorgehensweise[Bearbeiten | Quelltext bearbeiten]
Für bipartite Graphen gilt, das sie keine Kreise in ungerader Anzahl besitzen. Des weiteren kann man bipartite Graphen mittels Tiefensuche bestimmen, durch 2-Färbung. Dadurch kann man auch gleich die Partitionen des Graphen bestimmen.
Vorgehensweise bei dieser Lösung[Bearbeiten | Quelltext bearbeiten]
Einfach händisch mit 2 Stiften immer die einzelnen Knoten anmalen. Man sucht sich einen Knoten an bei dem man anfangen will und malt ihn in der ersten Farbe an. Sobald man dann eine Kante entlangwandert wechselt man den Stift und malt die nächste Kante in einer anderen Farbe an. Sollte man auf ein Knoten treffen der schon angemalt ist und dieser ist aber in der andern Farbe angemalt als man eigentlich jetzt benutzen müsste, so hat man einen bipartiten Graphen gefunden. Hat man alle Knoten angemalt und es trat dieser Effekt nie auf, so ist der Graph bipartit.
Graphische Anwendung der Vorgehensweise[Bearbeiten | Quelltext bearbeiten]
