TU Wien:Algorithmen und Datenstrukturen 1 VU (Raidl)/Übungen SS09/Beispiel 33

Der im Folgenden gezeigt Algorithmus von Dijkstra ist ein Klassiker um in einem gewichteten, ungerichteten Graphen G = (V,E) den kürzesten Pfad (Kantenzug) von einem Startknoten $s\in V$ zu einem Zielknoten $t\in V$.

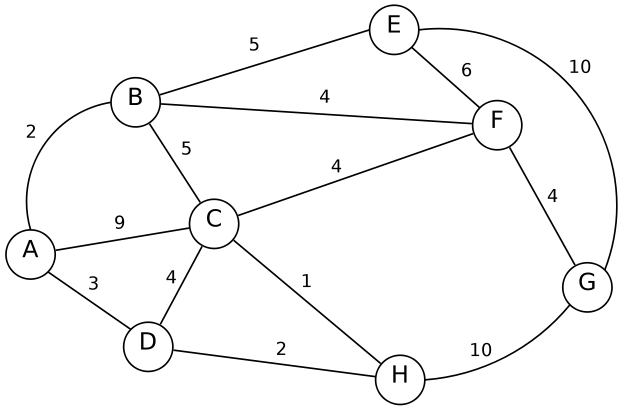
Wenden Sie diesen Algorithmus auf den nachstehenden Graphen an (die Kantenbeschriftungen entsprechen den Distanzen zwischen den verbundenen Knoten). Visualisieren Sie dabei alle Iterationsschritte des Verfahrens und geben Sie anschließend den kürzesten Weg (die einzelnen Kanten sowie die Gesamtlänge) vom Knoten A zum Knoten G an.

für alle knoten v ∈ V {
  d[v] = ∞; // Distanz des kürzesten Kantenzuges von s nach v
  p[v] = undef ; // Vorgänger am Pfad von s zu v
}
d[s] = 0;
Q = V ;
solange Q nicht leer {
  Entnimm jenes u aus Q mit minimalem d[u];
  falls d[u] = ∞ dann {
    Abbruch: Es existiert kein Pfad von s nach t.
  }
  falls u = t dann {
    Ausgabe: d[t];
    solange t = undef {
      Ausgabe: t;
      t = p[t];
    }
    Abbruch: Kürzester Kantenzug gefunden;
  }
  für alle e = (u, v) mit v ∈ N (u) {
    // w(e): Gewicht der Kante e
    falls d[v] > d[u] + w(e) dann {
      d[v] = d[u] + w(e);
      p[v] = u;
    }
  }
}

Lösung

Dijkstra-Algorithmus

A	B	C	D	E	F	G	H	Wahl	Vorgänger
0	∞	∞	∞	∞	∞	∞	∞	A	-
	2	9	3	∞	∞	∞	∞	B	A
		7	3	7	6	∞	∞	D	A
		7		7	6	∞	5	H	D
		6		7	6	15		F	B
		6		7		10		G	F

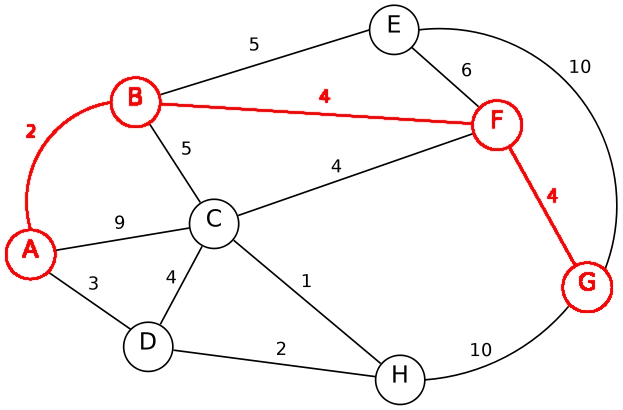
Demnach ist der beste Weg von A (0) -> B (2 = 0 + 2) -> F (6 = 0 + 2 + 4) -> G (10 = 0 + 2 + 4 + 4).

Graphische Lösung