TU Wien:Mathematik 2 UE (diverse)/Übungen SS07/Beispiel E3

Die Punkte (0, 0, 0), (0, 0, 2), (1, 0, 0) und (0, 1, 0) seien die Eckpunkte eines Tetraeders. Bestimmen Sie dessen Volumen mit Hilfe eines geeigneten Bereichsintegrals.

Lösungsversuch von Baccus

Graphische Darstellung

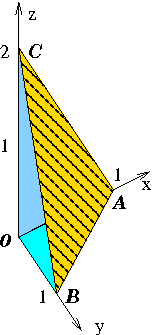
Der durch die gegebenen Eckpunkte definierte Tetraeder ist kein "gleichmäßiger", vielmehr eher eine "Viertel-Pyramide" um den Ursprung.

Graphenanalytische Abschätzung

Eine graphische Analyse liefert das Ergebnis:

Volumen (Pyramide) $V={\tfrac {1}{3}}\cdot G\cdot h$,   $G={\tfrac {1}{2}}\cdot 1\cdot 1$,   $h=2$:  $\Longrightarrow V={\tfrac {1}{3}}\cdot {\tfrac {1\cdot 1}{2}}\cdot 2={\frac {1}{3}}$.

Das zu erwartende Ergebnis steht also fest.

Integration

Wir integrieren ein Bereichsintegral über der Grundfläche AB0 (Skizze) mit der Funktion (Ebene $\varepsilon$):

Aus dem Graphen kann man die Ebenengleichung $\varepsilon$ für ABC fast direkt ablesen:

• Startvektor x,y=0: z=2
• Dreieck y=0 (AC0): Gerade ${\overline {AC}}=2-2x$
• Dreieck x=0 (BC0): Gerade ${\overline {BC}}=2-2y$

$\Longrightarrow \varepsilon =2-2x-2y$.

Über diese Gleichung setzen wir unser Integral an:

$\int _{0}^{1}\left(\int _{0}^{1-x}2-2x-2y\;dy\right)dx=$

(die obere Grenze des inneren Integrals ist $1-x$ (Dreiecks-Grundfläche AB0, Skizze))

${\begin{aligned}&=\left.\int _{0}^{1}2y-2xy-y^{2}\right|_{0}^{1-x}dx=\\&=\int _{0}^{1}\underbrace {2-2x-2x+2x^{2}-1+2x-x^{2}} _{1-2x+x^{2}}\;dx=\\&=\int _{0}^{1}(x-1)^{2}\;dx=\\&=\left.{\frac {(x-1)^{3}}{3}}\right|_{0}^{1}={\frac {1}{3}}\quad \surd \end{aligned}}$

Stimmt mit der graph.anal. Abschätzung eigentlich gut überein :-)

QED

--Baccus 23:10, 16. Mai 2007 (CEST)

Links

• Diskussion im Informatik-Forum

Wikipädia:

• Tetraeder
• Volumen (Pyramide)