TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 195
Zur Navigation springen
Zur Suche springen
In einer Menge von n Personen können 10 Personen Deutsch, 9 Englisch, 9 Französisch, 5 Englisch und Deutsch, 7 Deutsch und Französisch, 4 Englisch und Französisch, 3 alle Sprachen und niemand keine der drei Sprachen. Wie groß ist n?
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
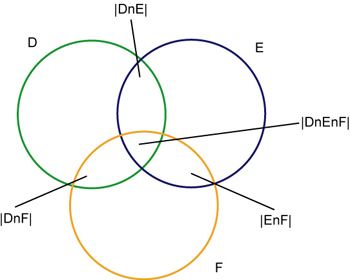
- Menge aller Personen die Deutsch können ist D,
- Menge aller Personen die Englisch können ist E,
- Menge aller Personen die Französisch können ist F,
- Menge aller Personen die Englisch und Deutsch können
- Menge aller Personen die Französisch und Deutsch können
- Menge aller Personen die Französisch und Englisch können
- Menge aller Personen die Deutsch, Französisch und Englisch können
- Menge aller Personen, die weder Deutsch, Französisch und Englisch können:
Inklusions-Exklusionsprinzip:
Grafische Darstellung:
Siehe auch: Beispiel_159