TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 424
Man zeige, dass für eine beliebige Menge M die Algebra ein kommutativer Ring mit Einselement ist. Für welche M ist dieser Ring sogar ein Körper?
Definition der symmetrischen Differenz[Bearbeiten | Quelltext bearbeiten]
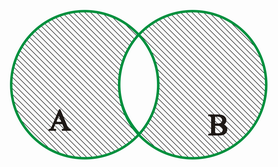
C heißt symmetrische Differenz der Mengen A und B,
,
wenn C alle Elemente aus A enthält, die nicht zu B gehören und alle Elemente aus B, die nicht zu A gehören, d.h.:
VENN-Diagramm:
Theoretische Grundlagen (Zusammenfassung von mnemetz)[Bearbeiten | Quelltext bearbeiten]
Gesetze und Eigenschaften von algebraischen Strukturen
Eine algebraische Struktur ist eine nichtleere Menge G mit einer oder mehreren Operationen.
Folgende Eigenschaften kann eine solche Struktur annehmen:
- Abgeschlossenheit: , für (d.h. ist eindeutig zugeordnet). Das entspricht einer Funktion von
- Assoziativgesetz: für alle .
- Einheitselement: Es existiert ein , so dass für alle gilt: .
- Inverses Element: Für jedes gibt es ein inverses Element (oder auch ) so, dass gilt . Wobei das e das Einheitselement ist.
- Kommutativgesetz: für alle .
Nr. Gruppoid Halbgruppe Monoid Gruppe Abelsche Gruppe 1 X X X X X 2 X X X X 3 X X X 4 X X 5 X
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Basierend auf f.thread:38144, etwas editiert und erweitert. --Mnemetz 03:33, 19. Dez 2005 (CET)
Für die symmetrische Differenz[Bearbeiten | Quelltext bearbeiten]
Abgeschlossenheit[Bearbeiten | Quelltext bearbeiten]
Wie schon aus den VENN-Diagrammen hervorgeht, ist eine Abgeschlossenheit gegeben.
Assoziativität[Bearbeiten | Quelltext bearbeiten]
Es liegt die Assoziativität vor!
Man könnte dies mit der Elementtafel nachweisen (Auszug):
| \ | \ | |||||||
| \ | \ | |||||||
| \ | \ |
neutrales Element (Einheitselement)[Bearbeiten | Quelltext bearbeiten]
Das neutrale Element existiert', es ist die leere Menge , denn .
Inverses Element[Bearbeiten | Quelltext bearbeiten]
Auch das inverse Element existiert, und zwar A' = A: jedes Element ist zu sich selbst invers.
Kommutativität[Bearbeiten | Quelltext bearbeiten]
Auch eine Kommutativität liegt vor.
- die symmetrische Differenz ist daher kommutativ
Schlussfolgerung[Bearbeiten | Quelltext bearbeiten]
Es liegt ein Abelsche Gruppe vor mit Nullelement .
Für den Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Abgeschlossenheit[Bearbeiten | Quelltext bearbeiten]
Falls : erfüllt
Assoziativität[Bearbeiten | Quelltext bearbeiten]
: erfüllt
neutrales Element (Einheitselement)[Bearbeiten | Quelltext bearbeiten]
: erfüllt für e = M -> Einselement
Inverses Element[Bearbeiten | Quelltext bearbeiten]
Existiert i.A. nicht, da für alle , d,h, für ist auch --- also ist für alle
Für ist allerdings , d.h. M hat ein Inverses.
Kommutativität[Bearbeiten | Quelltext bearbeiten]
: erfüllt
Schlussfolgerung[Bearbeiten | Quelltext bearbeiten]
ist ein kommutatives Monoid mit Einselement .
Distributivgesetze müssen gelten[Bearbeiten | Quelltext bearbeiten]
Am besten überprüft man das Gesetz, indem man die Mengen aufzeichnet, die Schnittmengen markiert und miteinander vergleicht. Analog dazu überprüft man auch das 2. Gesetz -> erfüllt.
Um ganz sicher zu gehen, sollte man sich die Elementtafel (s.o.) aufzeichnen. Man braucht auch nur eines der beiden Gesetze nachzuweisen, da abelsch ist.
Bei der algebraischen Struktur handelt es sich um einen kommutativen Ring mit Einselement.
Körperaxiome[Bearbeiten | Quelltext bearbeiten]
Das ist genau dann ein Körper, wenn
Beweis:
Sei , dann ist . Es genügt zu zeigen, dass abelsche Gruppe ist. Es ist . Damit ist das bereits eine abelsche Gruppe.
Sei umgekehrt abelsche Gruppe, dann existiert zu jedem ein Inverses in , was nach 4.2.4 bedeutet, dass , d.h. .
(Für ist , d.h. kein Gruppoid.)