TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 582
a) Für welche ist die Matrix A singulär?
b) Bestimmen Sie für die inverse Matrix .
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Für eine -Matrix, lässt sich die Determinante wie folgt berechnen:
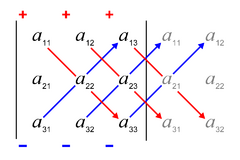
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Eine Matrix, die nicht invertierbar ist, wird singulär genannt. Bei einer solchen ist die Determinante also 0.
Zu zeigen ist nun, für welches die vorliegende Matrix nun singulär ist!
Damit singulär ist, muss gelten:
Es gibt kein also Lösung, sondern nur ein , daher ist die Matrix A für alle invertierbar!
Anmerkung (mjung): oben hast du bei der Gleichung einfach das x weggelassen. Das ist aber auch eine Nullstelle, also falls x = 0, ist die Gleichung 0 was die Matrix singulär machen würde. 0 ist Element von Q. In der Lösung hast hast du dann 0 aber weggelassen. So stimmt's auch, nur die letzte Bemerkung ist ein bisschen verwirrend.