TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 302

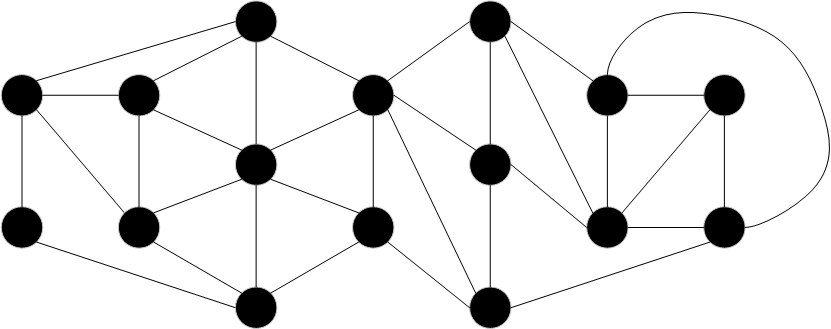
Man untersuche, ob der Graph $G_{14}$ eine Eulersche Linie besitzt, und bestimme gegebenenfalls eine.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Hilfreiches

Es gibt zwei Arten von eulersche Linie, eine offene und eine geschlossene. Eine geschlossene Euler'sche Linie gibt es in einem Graphen ungerichteten G, wenn G zusammenhängend ist und alle Knotengrade d(υ) (υ ∈ V(G)) gerade sind.

Eine offene Euler'sche Linie gibt es in einem Graphen ungerichteten G, wenn G zusammenhängend ist und mit der Ausnahme von zwei Knoten ω1, ω2 ∈ V(G) mit ungeradem Knotengrad und alle übrigen Knotengrade d(υ) (υ ∈ V(G) \ {ω1, ω2}) gerade sind

Lösungsvorschlag von Gamer199

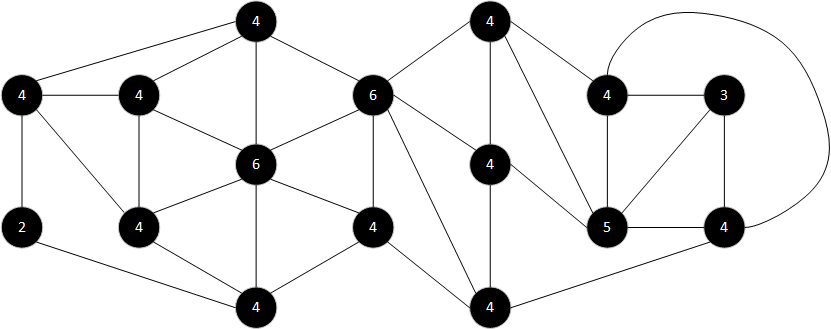
Zuerst müssen die Knotengrade bestimmt werden.

Man erkennt es gibt nur gerade Knotengrade, die Ausnahme sind genau 2 Knoten mit einem ungeraden Knotengrad. Daraus erkennt man es gibt eine offene Euler'sche Linie.

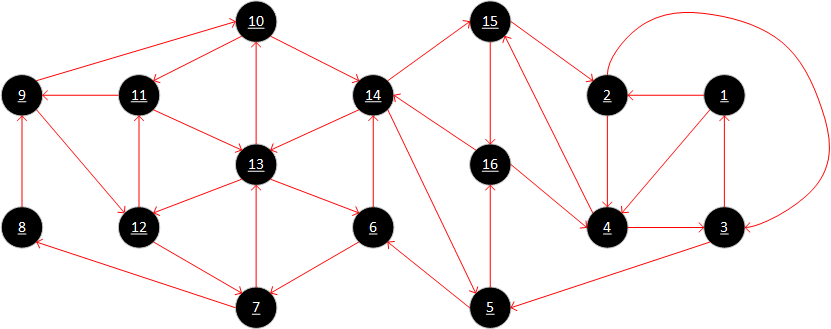
Um diese nun zu Konstruieren muss man jede Kante einmal verwenden und jeden Knoten erreichen. Man beginnt bei einem Knoten mit einem ungeraden Knotengrad und hört bei dem zweiten Knoten mit ungeradem Knotengrad wieder auf.

Ein Beispiel für eine Euler'sche Linie ist in folgender Grafik zu finden, wenn es eine Euler'sche Linie gibt, kann man auch viele weitere Euler'sche Linien finden.

$1\Rightarrow 2\Rightarrow 3\Rightarrow 1\Rightarrow 4\Rightarrow 3\Rightarrow 5\Rightarrow 6\Rightarrow 7\Rightarrow 8\Rightarrow 9\Rightarrow 10\Rightarrow 11\Rightarrow 9\Rightarrow 12\Rightarrow 11\Rightarrow 13\Rightarrow 12\Rightarrow 7\Rightarrow 13\Rightarrow 10\Rightarrow 14\Rightarrow 13\Rightarrow 6\Rightarrow 14\Rightarrow 15\Rightarrow 2\Rightarrow 4\Rightarrow 15\Rightarrow 16\Rightarrow 14\Rightarrow 5\Rightarrow 16\Rightarrow 4$