TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 319

Man zeige, dass die Anzahl der binären Suchbäume mit n Knoten durch die Catalan-Zahl $C_{n}$ gegeben ist. (Hinweis: Man stelle eine Bijektion zwischen binären Suchbäumen und (geordneten) vollen Binärbäumen her und verwende das vorherige Beispiel.)

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag von Ryus

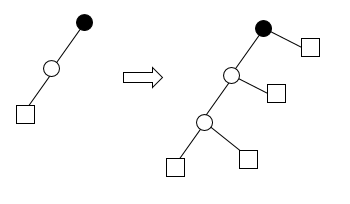
Der Unterschied zwischen normalen binären Bäumen und vollen binären Suchbäumen ist, dass in binären Suchbäumen nicht jeder Knoten entweder keine oder zwei Nachfolger haben muss, sondern auch nur einen haben kann, wobei man jedoch dazwischen unterscheidet, ob der Nachfolger links oder rechts vom aktuellen Knoten ist.

In Beispiel 313 wurde bereits bewiesen, dass die Anzahl der vollen Binärbaum mit n+1 Blättern der n-ten Catalan-Zahl entspricht. Wenn wir es also schaffen, eine Bijektion zu finden, welche von einem binären Suchbaum mit n Knoten zu einem Binärbaum mit n+1 Blättern führt, haben wir damit auch sofort gezeigt, dass die Anzahl der binären Suchbäume mit n Knoten durch die n-te Catalan Zahl gegeben ist.

Dazu überlegen wir uns folgendes Verfahren: Wir nehmen den binären Suchbaum und fügen an jeden Knoten, der nicht zwei Nachfolger hat, so viele Nachfolger wie möglich (also maximal 2) an. So erhalten wir einen entsprechenden Baum mit n+1 Blättern. Diese Funktion ist bijektiv, da wir von jedem Baum mit n+1 Blättern auf einen Baum mit n Knoten kommen können, in dem wir diese Blätter einfach wieder entfernen.

In Beispiel 310 wurde gezeigt, dass die Anzahl der Blätter eines Binärbaumes gleich der Anzahl der internen Knoten + 1 ist. Durch unsere Abbildung werden alle n Knoten zu internen Knoten. Die Anzahl der Blätter im so entstandenen neuen Baum muss daher n+1 sein!

Somit ist die Bijektion gefunden und die Aussage bewiesen.