TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 285
Konstruieren Sie, wenn möglich, einen ungerichteten Graphen mit den Graden
a) 2, 2, 3, 3, 4, 4
b) 2, 3, 3, 4, 4, 4
c) 2, 3, 3, 3, 4, 4
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theoretische Grundlagen (von mnemetz)[Bearbeiten | Quelltext bearbeiten]
Ein Graph G ist ein Tupel (V, E), wobei V eine Menge von Knoten (englisch vertex, oft auch Ecken genannt) und E eine Menge von Kanten (englisch edge, manchmal auch Bögen genannt) bezeichnet. Dabei ist E in
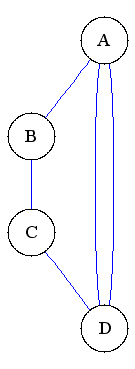
- ungerichteten Graphen ohne Mehrfachkanten eine Teilmenge aller 2-elementigen Teilmengen von V,
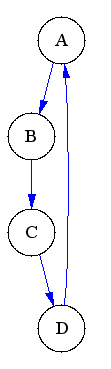
- gerichteten Graphen ohne Mehrfachkanten eine Teilmenge des kartesisches Produkt|kartesischen Produktes V x V,
- ungerichteten Graphen mit Mehrfachkanten eine Multimenge über der Menge aller 2-elementigen Teilmengen von V,
- gerichteten Graphen mit Mehrfachkanten eine Multimenge über dem kartesischen Produkt V x V,
- Hypergraphen eine Teilmenge der Potenzmenge von V.
 |
 |
 |
 |
Somit können wir in den Aufgabenstellungen einen ungerichten Graphen ohne Mehrfachkanten nur dann zeichnen, wenn das Handschlaglemma gilt: Die Summe über die Grade aller Knoten eines Graphen ist gleich der doppelten Kantenanzahl in dem Graphen.
Da die doppelte Kantenanzahl gerade ist, muss die Summe über die Grade aller Knoten auch gerade sein. In der Summe darf ich beliebig Klammern setzen, also auch einmal um alle geraden Summanden (diese Summe ist auf jeden fall gerade), und dann einmal um alle ungeraden Summanden; damit die zweite Summe gerade ist, muss die anzahl deren Summanden gerade sein. Nun ist aber jeder Summand Grad eines Knotens; diese Knoten haben alle ungeraden Grad; d.h. die Anzahl der Knoten mit ungeradem Grad ist gerade.
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Beispiel a[Bearbeiten | Quelltext bearbeiten]
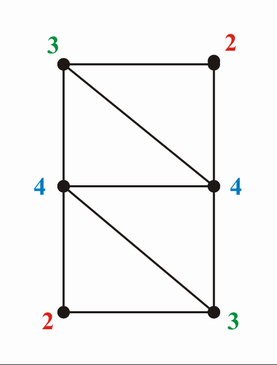
Grade: 2, 2, 3, 3, 4, 4
Gerade Anzahl ungerader Knotengrade kann gezeichnet werden!
Beispiel b[Bearbeiten | Quelltext bearbeiten]
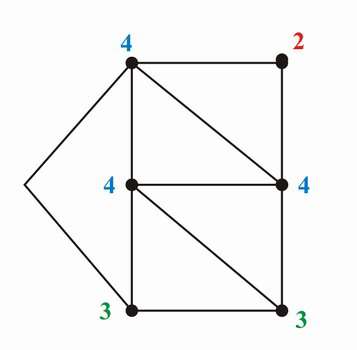
Grade: 2, 3, 3, 4, 4, 4
Gerade Anzahl ungerader Knotengrade kann gezeichnet werden!
Beispiel c[Bearbeiten | Quelltext bearbeiten]
Grade: 2, 3, 3, 3, 4, 4
Ungerade Anzahl ungerader Knotengrade: kann nicht gezeichnet werden!