TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 318
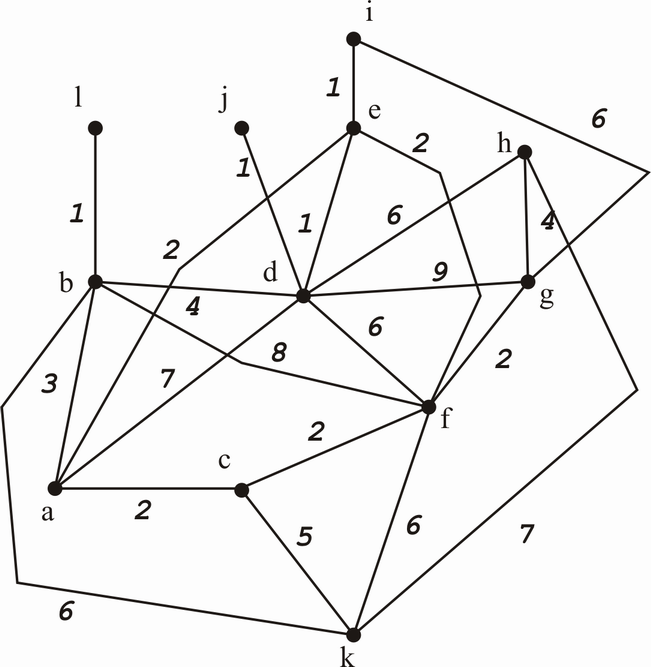
Gegeben sei ein ungerichteter, zusammenhängender, bewerteter Graph mit durch seine Kanten / Bewertungen:
ab/3, ac/2, ad/7, ae/2, bd/4, bf/8, bk/6, bl/1, cf/2, ck/5, de/1, df/6, dg/9, dh/6, dj/1, ef/2, ei/1, fg/2, gh/4, fk/6, gi/6, hk/7. (a) Man gebe drei verschiedene Gerüste von an.
(b) Man bestimme ein Minimalgerüst von und dessen Gesamtlänge .
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Skizze[Bearbeiten | Quelltext bearbeiten]
Skizze, aktualisiert. --Mnemetz 13:24, 6. Dez 2005 (CET)
Lösungsvorschlag von deez[Bearbeiten | Quelltext bearbeiten]
Also ich hab die Kanten geordnet: bl/1, de/1, dj/1, ei/1,
ac/2, ae/2 cf/2, ef/2, fg/2,
ab/3,
bd/4, gh/4,
ck/5,
bk/6, df/6, dh/6, fk/6, gi/6,
hk/7 ad/7
bf/8,
dg/9,
Und bin dann auf folgenden Graph gekommen: bl/1, de/1, dj/1, ei/1,
ac/2, ae/2 cf/2, ef/2, fg/2,
ab/3,
bd/4, gh/4,
ck/5
und bin dabei nie auf einen Kreis gestoßen. Ist alles zusammen falsch, da ich irgndwie von einem gerichteten Graph ausgegangen bin!! Tut mir sehr leid!
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Gerüste[Bearbeiten | Quelltext bearbeiten]
Ein Spannbaum (synonym auch aufspannender Baum oder kürzer spannender Baum; englisch spanning tree) ist in der Graphentheorie ein Teilgraph eines ungerichteten Graphen, der ein Baum ist und alle seine Knoten enthält. Spannbäume existieren nur in zusammenhängenden Graphen.
Einen Teilgraphen, der in (nicht notwendigerweise zusammenhängenden) Graphen für jede Komponente einen Spannbaum ergibt, nennt man Gerüst, Spannwald, aufspannender Wald oder kürzer spannender Wald. In zusammenhängenden Graphen sind Gerüst und Spannbaum also identische Begriffe, während Spannbäume für unzusammenhängende Graphen nicht definiert sind.
In kantengewichteten Graphen lässt sich als Gewicht eines Graphen die Summe seiner Kantengewichte definieren. Ein Spannbaum bzw. ein Gerüst heißt minimal, wenn kein anderer Spannbaum bzw. kein anderes Gerüst in demselben Graphen mit geringerem Gewicht existiert. Häufig kürzt man minimaler Spannbaum auch mit MST (Abkürzung des englischen Begriffs Minimum Spanning Tree) ab. Statt minimales Gerüst sagt man auch Minimalgerüst.
Anders gesagt: Ein Gerüst eines Graphen liegt als Teilgraph von G vor, wenn es ein Baum ist und V'=V erfüllt, d.h. die beiden Knotenmengen sind gleich gross (= die Anzahl der Knoten).
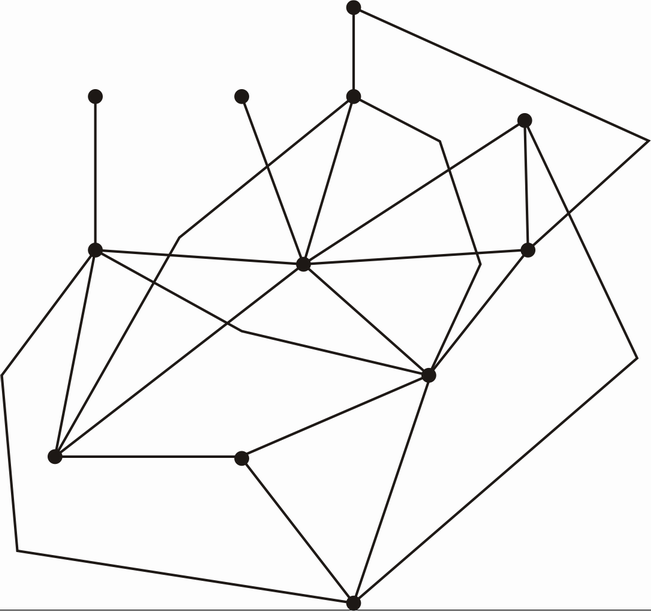
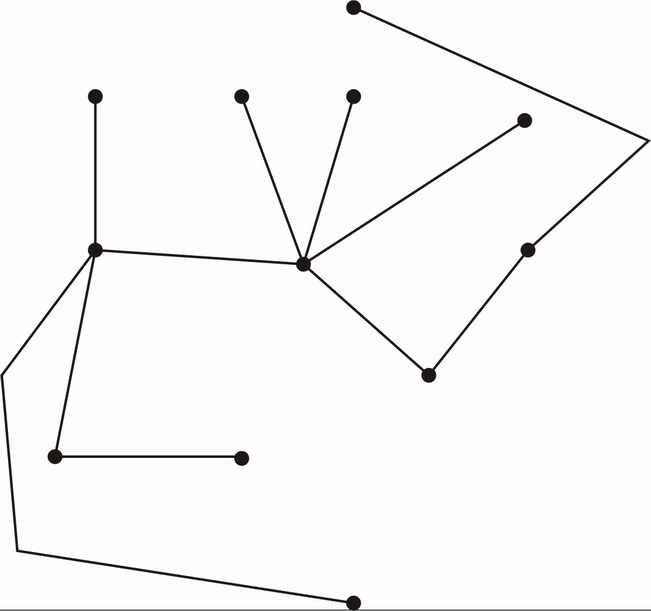
Der ganze Graph (Ohne Gewichte, Punktbezeichnungen - die sind nun nicht wichtig):
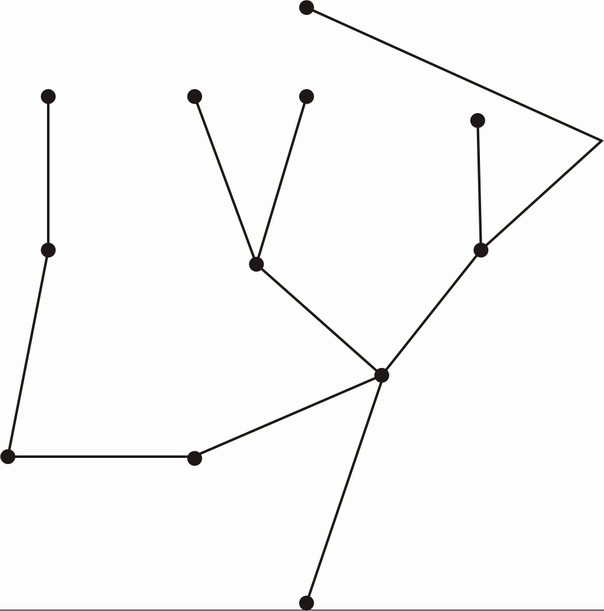
Drei Lösungen, die alle Kreise eliminieren und die Anzahl der Knoten gleich halten. Ich habe der Einfachheit halber zusammenhängende Gerüste erstellt!
Ach leck mich doch ... eine Kante umstellen :-)
Und eine "Schlange" :-)
Minimalgerüst[Bearbeiten | Quelltext bearbeiten]
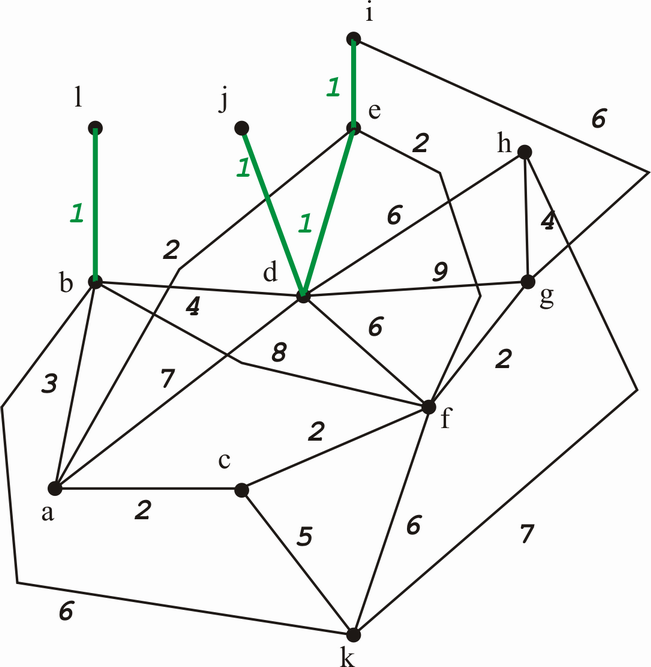
Es wird der Algorithmus von Kruskal verwendet. Zunächst sortierte ich die Kanten nach ihrer Bewertung:
1 (b,l) (d,e) (d,j) (e,i) 2 (a,c) (a,e) (c,f) (e,f) (f,g) 3 (a,b) 4 (b,d) (g,h) 5 (c,k) 6 (b,k) (d,f) (d,h) (f,k) (g,i) 7 (a,d) (h,k) 8 (b,f) 9 (d,g)
Dann legen wir mal die 1-er Kanten aneinander - sie bilden keinen Kreis. Bitte, im Normalfall geht man von einer leeren Menge aus - die Zeichnungen zeigen alles (hat verarbeitungstechnische Gründe).
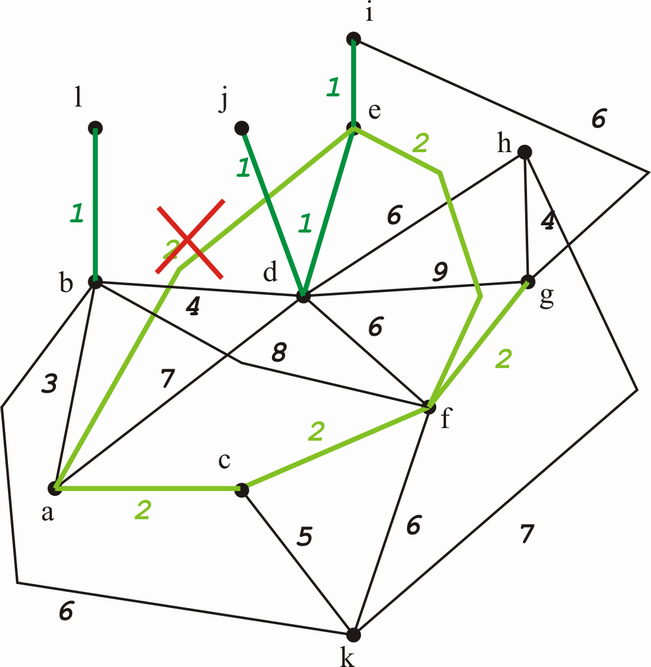
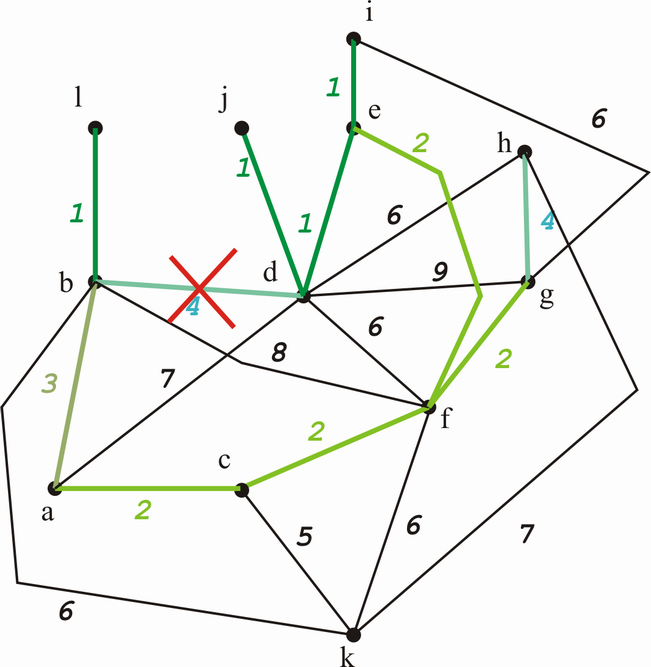
Nun legen wir die 2-er Kanten aneinander. Da ein Kreis gebildet wird, entfernen wir (a,e).
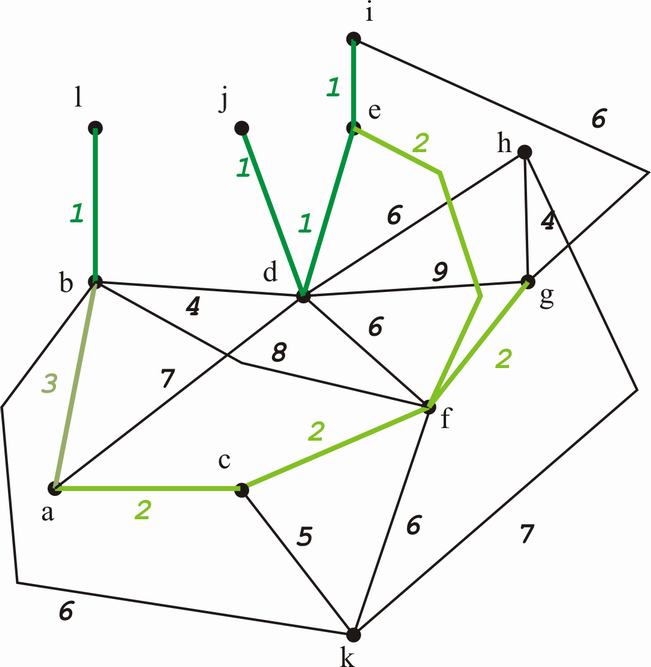
Der nächste Schritt ist klar. (a,b) wird hinzugefügt und es kann bleiben - kein Kreis entsteht.
Nun fügen wir die 2 Vierer-Kanten an. (b,d) bildet einen Kreis und wird daher ausgeschlossen.
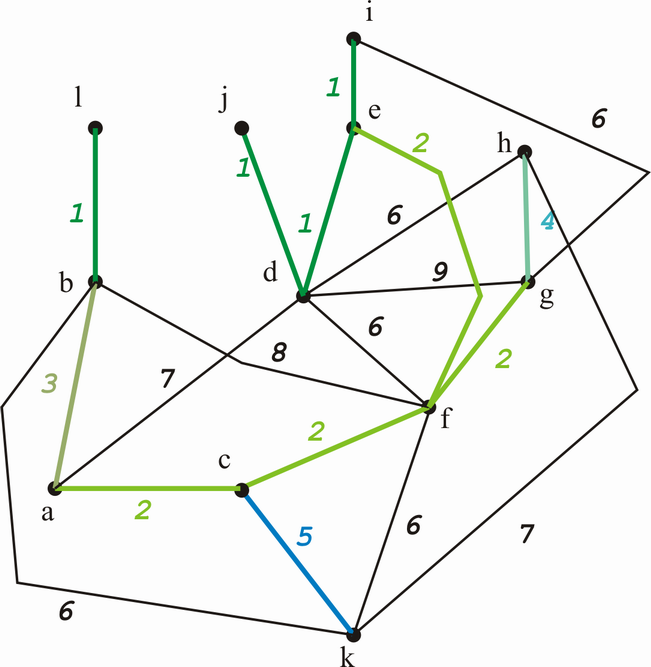
Nun die 5-er Kante. Wiederum wird kein Kreis gebildet
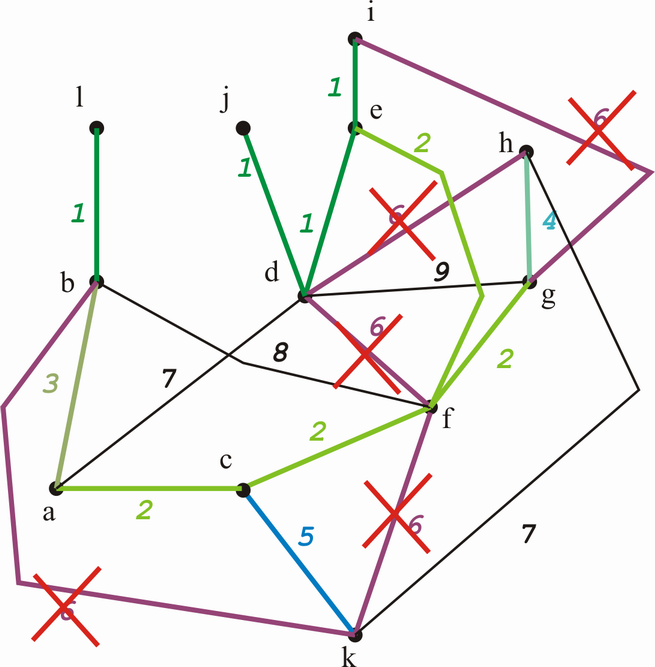
Alle 6-er Kanten bilden einen Kreis => ausgeschlossen!
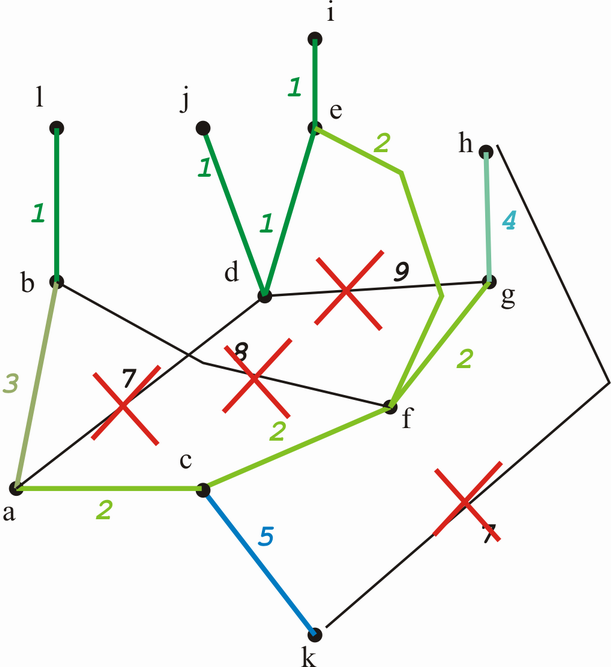
Wie man leicht sehen kann, bilden die Kanten 7-9 jeweils Kreise ...
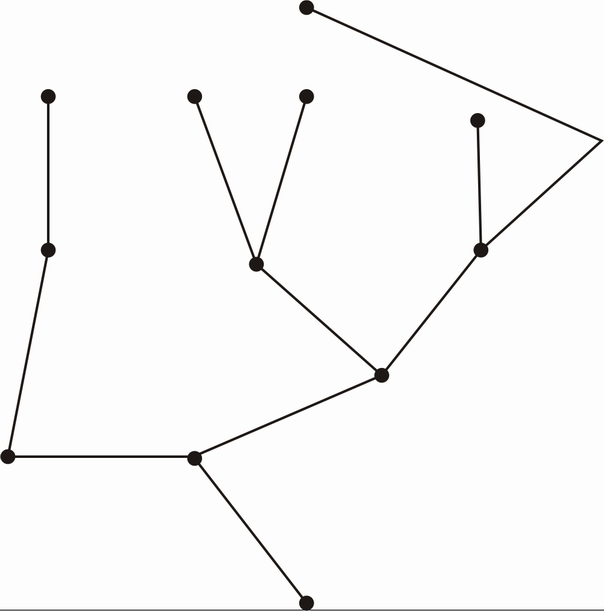
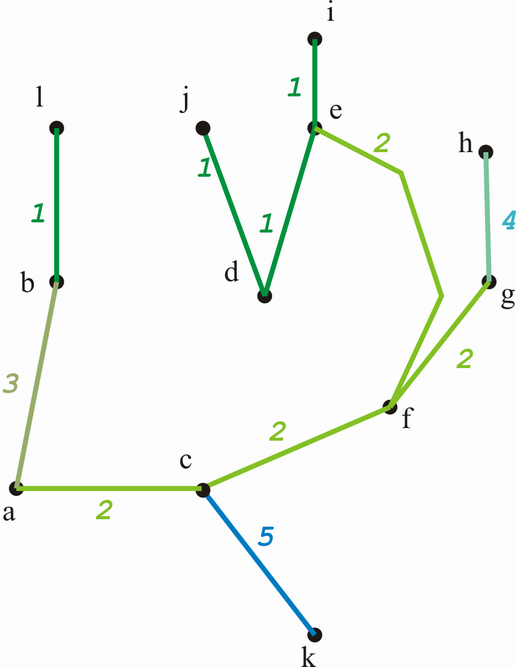
Das Minimalgerüst ist also:
Die Länge des Minimalgerüsts beträgt 24.