TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 597

Für die Vektoren ${\vec {x}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}$, ${\vec {y}}={\begin{pmatrix}3\\-1\\2\end{pmatrix}}$ und ${\vec {z}}={\begin{pmatrix}2\\2\\1\end{pmatrix}}$ berechne man

1. die Längen von ${\vec {x}}$,${\vec {y}}$ und ${\vec {z}}$
2. den Winkel $\phi$ zwischen ${\vec {x}}$ und ${\vec {y}}$
3. das Volumen des von ${\vec {x}}$,${\vec {y}}$ und ${\vec {z}}$ aufgespannten Parallelepipeds

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag von mnemetz

Längen der Vektoren

Die Länge eines Vektors wird bestimmt durch: $|{\vec {v}}|={\sqrt {a_{1}^{2}+a_{2}^{2}+\dots +a_{n}^{2}}}$.

• $|{\vec {x}}|={\sqrt {1^{2}+2^{2}+3^{2}}}={\sqrt {1+4+9}}={\sqrt {\mathit {14}}}$
• $|{\vec {y}}|={\sqrt {3^{2}+1^{2}+2^{2}}}={\sqrt {9+1+4}}={\sqrt {\mathit {14}}}$
• $|{\vec {z}}|={\sqrt {2^{2}+2^{2}+1^{2}}}={\sqrt {4+4+1}}={\sqrt {9}}={\mathit {3}}$

Winkel zwischen den Vektoren

Der Winkel zwischen den Vektoren ergibt sich aus der Formel (Cosinussatz):

• ${|{\vec {x}}-{\vec {y}}|}^{2}={|{\vec {x}}|}^{2}+{|{\vec {y}}|}^{2}-2*|{\vec {x}}|*|{\vec {y}}|*\cos \phi \qquad \Rightarrow \qquad \cos \phi ={\frac {{\vec {x}}*{\vec {y}}}{|{\vec {x}}|*|{\vec {y}}|}}$

Somit ergibt sich:

$\cos \phi ={\frac {{\begin{pmatrix}1\\2\\3\end{pmatrix}}*{\begin{pmatrix}3\\-1\\2\end{pmatrix}}}{{\sqrt {14}}*{\sqrt {14}}}}={\frac {3-2+6}{14}}={\frac {7}{14}}={\frac {1}{2}}$

$\phi ={\frac {\pi }{3}}=60^{\circ }$

Zur Erinnerung - die Umrechnungsformelm: Zuerst Angabe in Grad, danach in Bogenmaß. Die Umrechnungsformeln sind:

• Von Grad nach Bogenmaß:

${\rm {Winkel}}_{\rm {Bogenmass}}={\frac {{\rm {Winkel}}_{\rm {Grad}}\cdot \pi }{180}}$

• Von Bogenmaß nach Grad:

${\rm {Winkel}}_{\rm {Grad}}={\frac {{\rm {Winkel}}_{\rm {Bogenmass}}\cdot 180}{\pi }}$

Volumen des Parallelepipeds

Schematisch die Problemstellung:

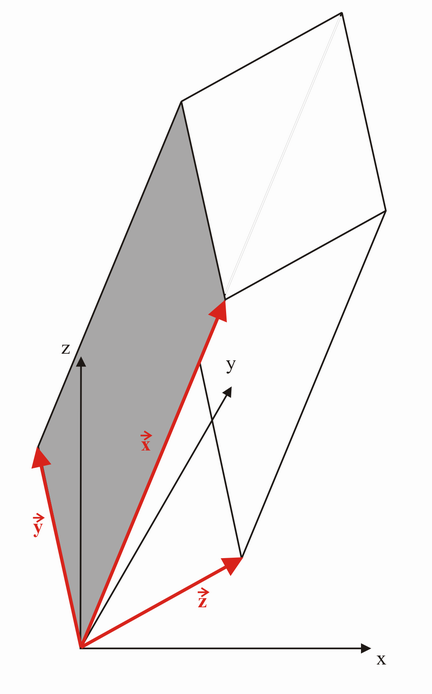
Das Volumen errechnet sich aus dem äusseren Produkt (Spatprodukt) der Vektoren ${\vec {x}}$ und ${\vec {y}}$, was wiederum einen Vektor ergibt. Dieser Vektor wird mit ${\vec {z}}$ multipliziert - das sich ergebende Skalar ist das Volumen.

Zur Erinnerung: Das Spatprodukt errechnet sich wie folgt:

(Anm: Eigentlich ist das Spatprodukt von ${\mathfrak {x}},{\mathfrak {y}},{\mathfrak {z}}$ so definiert (der Rechenweg bleibt aber richtig): $\det({\mathfrak {x}},{\mathfrak {y}},{\mathfrak {z}})$ oder eben $\langle {\mathfrak {x}}\times {\mathfrak {y}},{\mathfrak {z}}\rangle$. )

${\vec {x}}={\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}},{\vec {y}}={\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}\Rightarrow {\vec {x}}\times {\vec {y}}={\begin{pmatrix}{\begin{vmatrix}x_{2}&y_{2}\\x_{3}&y_{3}\end{vmatrix}}\\-{\begin{vmatrix}x_{1}&y_{1}\\x_{3}&y_{3}\end{vmatrix}}\\{\begin{vmatrix}x_{1}&y_{1}\\x_{2}&y_{2}\end{vmatrix}}\end{pmatrix}}$

Somit müssen wir berechnen:

$({\begin{pmatrix}1\\2\\3\end{pmatrix}}\times {\begin{pmatrix}3\\-1\\2\end{pmatrix}})*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}{\begin{vmatrix}2&-1\\3&2\end{vmatrix}}\\-{\begin{vmatrix}1&3\\3&2\end{vmatrix}}\\{\begin{vmatrix}1&3\\2&-1\end{vmatrix}}\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}4+3\\-(2-9)\\-1-6\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}7\\7\\-7\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}=14+14+7={\mathit {35}}$

Gehört hier nicht: 14 + 14 - 7 = 21 ????? nein weil wir einen Betrag suchen ! --Zool 15:42, 1. Feb. 2009 (UTC) - Doch, das Ergebnis ist 21. Der Betrag wird am Ende genommen, irgendwann beliebig zwischendurch Vorzeichen weglassen ist absoluter Unsinn.

es gehört aber der Betrag des Ergebnisses genommen und nicht jeder Term in der Gleichung positiv gesetzt
Das kommt daher, dass der Vektor ja auch nach im Raum "nach unten" gehen kann und damit das Volumen negativ wird (was nicht geht).
Deshalb nimmt man als Ergebnis einfach ein positives Vorzeichen

alternativer Lösungsweg von Persie0

Manch ein Tutor will lieber den Weg über die Determinante sehen.

Mit der Formel (ist auch im Buch) von Wikipedia: Für ${\vec {a}}=(a_{1},a_{2},a_{3})^{T},\quad {\vec {b}}=(b_{1},b_{2},b_{3})^{T},\quad {\vec {c}}=(c_{1},c_{2},c_{3})^{T}$ ist das Volumen dann:

$V=\left|\det {\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}}\;\right|$

also der Betrag der Determinante ist das Volumen.

In unserem Fall:

$V=\left|\det {\begin{pmatrix}1&3&2\\2&-1&2\\3&2&1\end{pmatrix}}\;\right|$

Anschließend kann man sich mit dem Gaußschen Eliminationsverfahren zur Determinantenberechnung die Determinante einfach ausrechnen, wobei 21 das Ergebnis ist.