TU Wien:Algorithmen und Datenstrukturen 1 VU (Raidl)/Übungen SS09/Beispiel 30

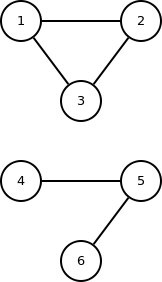
(a) Gegeben sei der folgende ungerichtete Graph

G = (V,E) mit V = {1,2,3,4,5,6} und

E = {(1,2),(1,3),(2,3),(4,5),(5,6)}

Zeichnen Sie den Graphen. Ist der Graph ein Baum oder ein Wald (Wald: kreisfreier Graph; Baum: zusammenhängender kreisfreier Graph)? Wieviele Kanten müssen Sie mindestens hinzufügen bzw entfernen um aus dem Graphen einen Baum bzw. einen Wald zu machen?

(b) Erstellen Sie einen ungerichteten Graphen mit 7 Knoten, bei dem jeder Knoten den Grad 3 hat, oder beweisen Sie, dass das nicht möglich ist.

(c) Beweisen oder widerlegen Sie: In jedem Graphen mit mindestens 2 Knoten existieren zwei Knoten u,v mit $u\neq v$ und d(u) = d(v).

Lösung

Teil A

Erster Teil

Die Graphen ist weder Wald noch Baum.

Zweiter Teil

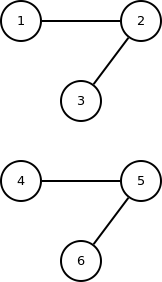
Durch entfernen einer Kante im Graphen mit dem Kreis, entstehen 2 kreisfreie Graphen. Jeder für sich ein Baum, demnach insgesamt ein Wald.

Dritter Teil

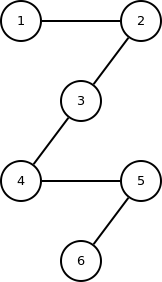
Durch hinzufügen einer Kante vom Knoten 3 zum Knoten 4 entsteht ein zusammenhängender, kreisfreier Graph. Auch Baum genannt.

Teil B

d(v) $\forall$ v = 3

$\sum$ d(v) = Anzahl der Knoten mal der Knotengrade. Demnach: 7 $\cdot$ 3 = 21

da aber 2 (pro Kante zwei Knoten) kein echter Teiler von 21 ist, ist dies nicht möglich.

Teil C

Wir konstruieren einen Graphen G für den folgendes gelten soll: Es existieren 2 Knoten v und w für die gilt d(v) = d(w)

• n = Anzahl der Knoten (V).
• alle v aus V haben andere Knotengrade , d.h. O-(n-1)

=> es existiert ein v aus V für das gilt d(v) = (n-1) => es existiert ein w aus V für das gild d(v) = 0 => v ist mit allen Knoten verbunden. => Widerspruch zur Behauptung es gibt einen Knoten mit d(w) = 0