TU Wien:Algorithmen und Datenstrukturen 1 VU (Raidl)/Übungen SS09/Beispiel 38

Gegeben ist ein Feld, das die folgenden Elemente in der angegebenen Reihenfolge enthält:

$\left\langle 40,20,1,2,3,30\right\rangle$

Handelt es sich hierbei um einen gültigen Maximum-Heap (das größte Element steht in der Wurzel)? Falls nicht führen Sie den ersten Teil des Heap-Sort Algorithmus durch, um einen gültigen Maximum-Heap zu bekommen.

Weiters soll die Folge aufsteigend sortiert werden. Führen Sie dazu auf dem erstellten Heap den zweiten Teil des Heap-Sort Algorithmus (die endgültige aufsteigende Sortierung) durch. Stellen Sie auch hier den Heap nach jedem Schritt als Feld (inklusive der bereits sortierten Zahlen) dar.

Begründen Sie in kurzen Worten, warum für die aufsteigende Sortierung eines Feldes ein Maximum-Heap verwendet werden sollte und nicht ein Minimum-Heap.

Lösung

Auf Maximum-Heap überprüfen

• einerseits kann der checkMaxHeap-Algorithmus von hier anwenden um es zu überprüfen.

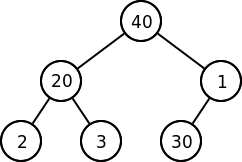
• andererseits kann sich einen leeren Heap aufzeichnen und ihn dann in Levelorder-Reihenfolge befüllen.\\

Man sieht gleich das eine Verletzung des Max-Heaps besteht. Um einen zu bekommen einfach 1 und 30 vertauschen.

Sortieren

$\left\langle 40,20,30,2,3,1\right\rangle$

Der sortierte Teil wird rechts vom Strich fett geschrieben. Die kursiven Zeilen zeigen jeweils die unsortierte Folge nach dem reorganisieren den Max-Heaps an.

40, 20, 30, 2, 3, 1 |

1, 20, 30, 2, 3 | 40

30, 20, 1, 2, 3 | 40

3, 20, 1, 2 | 40, 30

20, 3, 2, 1 | 40, 30

2, 3, 1 | 40, 30, 20

3, 2, 1 | 40, 30, 20

1, 2 | 40, 30, 20, 3

2, 1 | 40, 30, 20, 3

1 | 40, 30, 20, 3, 2

| 40, 30, 20, 3, 2, 1

Warum Maximum-Heap

Es wäre auch möglich einen Minimum-Heap zu verwenden und die sortierte Folge von Links nach Rechts aufbauen, aber dann müsste man den verbleibenden Heap immer um 1 nach rechts verschieben bzw ein zweites Feld anlegen, was von der Performance nicht optimal ist.