TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 127

Sei $f:[0,a]\rightarrow \mathbb {R}$ stetig, $f(0)=0$, $f(a)>a$ und $f(x)\neq x$ für $0<x<a$. Man zeige, dass dann auch $f(x)>x$ für $0<x<a$ gilt.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag von Nichtmax

Beweisidee

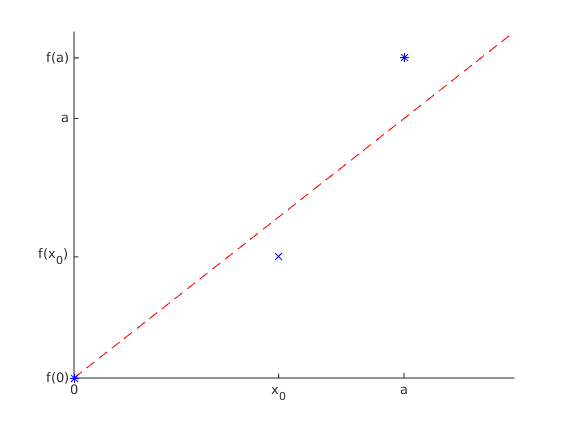
Eine Skizze wird hilfreich sein:

Wie auch immer $f$ aussieht, wir kennen den Funktionswert an der Stelle $0$ und wissen, dass der Funktionswert an der Stelle $a$, $f(a)$ über $a$ liegen muss. Außerdem wird anschaulich gesprochen, nie die 1. Mediane ($y=x$, die rot strichlierte Linie) getroffen.

Erneut anschaulich gesprochen, muss eine stetige Funktion "ohne Absetzen durchziehbar sein". Wenn die Funktion also irgendwo unter der 1. Mediane wäre (in der Skizze z.B. bei $x_{0}$, müsste sie irgendwann vor $a$ wieder über die Mediane kommen, wobei sie sie schneiden würde, was ein Widerspruch zu $f(x)\neq x$wäre.

Mathematischer Beweis

Es eignet sich ein indirekter Beweis. Wir nehmen an, dass es ein $x_{0}$ gibt, bei dem $f(x_{0})<x_{0}$ gilt, und führen die Annahme mithilfe der Eigenschaften stetiger Funktionen zu einem Widerspruch. Also:

Sei $x_{0}\in (0,a),f(x_{0})<x_{0}$. Weiters ist bekannt: $f(0)=0$, sowie $f(a)>a$.

Dazu äquivalent sind $f(x_{0})-x_{0}<0$ und $f(a)-a>0$. Das riecht schon nach einer Anwendung des Nullstellensatzes.

Dazu konstruieren wir zuerst noch eine neue Funktion

$g(x):=f(x)-x$.

Da $f$ stetig ist, ist auch $g$ stetig (Stetige Funktion minus einer anderen stetigen Funktion, in diesem Fall einer Konstante).

Einsetzen in $g$:

$g(a)=f(a)-a>0$

$g(x_{0})=f(x_{0})-x_{0}<0$.

Aus dem Nullstellensatz von Bolzano folgt nun: $\exists x_{1}\in (x_{0},a):g(x_{1})=0$.

Da aber $g(x_{1})=f(x_{1})-x_{1}=0$, folgt $f(x_{1})=x_{1}$. Damit haben wir einen Widerspruch zu der Voraussetzung $f(x)\neq x,0<x<a$.

Für alle $x$ ( $0<x<a$ ) kann daher nur mehr gelten, dass $f(x)>x$.