TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 376
(Weitergeleitet von TU Wien:Analysis UE (diverse)/Übungen SS19/Beispiel 358)
Man bestimme alle relativen Extrema und Sattelpunkte der Funktion im angegebenen Bereich:
für
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungshilfe[Bearbeiten | Quelltext bearbeiten]
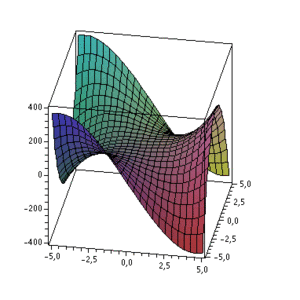
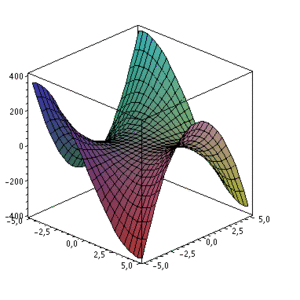
Nun setzt man beide Formeln gleich 0. Als erstes für x:
(das lösen wir jetzt nicht weiter auf, man sieht dann warum)
und dann für y:
Weiter geht't mit Einsetzen. Wir setzen nun das Ergebnis von y in die Formel von x ein:
Daraus folgt:
Das nun in die y-Formel eingesetzt ergibt:
- Luki (Komplette Lösung folgt)
Links[Bearbeiten | Quelltext bearbeiten]
- Diskussion im Informatik-Forum SS07 Beispiel 99
- Diskussion im Informatik-Forum WS07 Beispiel 124
Ähnliche Beispiele: