TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 116

Man zeichne den Graphen der Funktion f(x) und bestimme alle Stellen, an denen f(x) stetig ist.

$f(x)=(x^{2}-1)\operatorname {sgn}(\sin(\pi x))$

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag

Bild der Funktion

Intervall

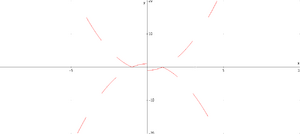
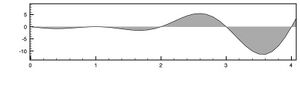
• Die Funktion ist symmetrisch entlang der X-Achse.
• Der Intervall ist immer gleich und hängt von der Periode von Sinus ab. Bei f(x)=sin(x) ist die Periode 2Pi, bei f(x)=sin(Pi*x) ist die Periode 2(2Pi/Pi).
• Die Funktion ist stetig steigend in den Bereichen: 0,5-1,5;2,5-3,5;...
• Die Funktion ist stetig fallend in den Bereichen: 0-0,5;1,5-2,5;...
• Für den negativen Bereich gilt wegen der X-Achsen Symmetrie genau dasselbe.

Lösungsvorschlag von Slaybert

$f(x)=g(x)*h(x)$

$g(x)=(x^{2}-1)$

$h(x)=\operatorname {sgn}(\sin(\pi x))$

g(x) ist stetig, weil Funktionsauswertung und Grenzwertbildung an jeder beliebigen Stelle das Gleiche liefert.

Da h(x) immer zwischen 1 und -1 wechselt ist h(x)g(x) immer stetig und entweder positiv oder negativ zwischen den Stellen an denen g(x) wechselt.

An den Stellen an denen g(x) wechselt (nämlich bei $x\in \mathbb {Z}$) ist f(x)=0, weil g(x)=0 laut Definition von sgn(x). An diesen Stellen springt f(x) erst auf Null und dann in den positiven/negativen Bereich.

f(x) ist also bei $x\in \mathbb {R} \backslash \mathbb {Z}$ stetig.

--Slaybert (Diskussion) 10:50, 27. Apr. 2013 (CEST)

Lösungsvorschlag von Tr4in

Die Funktion weist Lücken in fast allen ganzzahligen Punkten auf.

• In den Punkten 1 und -1 sieht es aus, dass die Funktion stetig ist.
• Im Punkt 0 jedoch sieht es so aus, dass die Funktion nicht stetig ist.

Ich habe die Punkte$(-1,0,1)$ mit links- und rechtsseitigen Grenzwerten untersucht:

• $x=-1$

Linksseitiger Grenzwert: $\lim \limits _{x\rightarrow -1^{-}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=0$

Rechtsseitiger Grenzwert: $\lim \limits _{x\rightarrow -1^{+}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=0$

Diese beiden Grenzwerte stimmen mit dem Funktionswert im Punkt $x=-1$ überein: $f(-1)=0$

$=>$ Somit ist die Funktion im Punkt $x=-1$ stetig.

• $x=1$

Linksseitiger Grenzwert: $\lim \limits _{x\rightarrow 1^{-}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=0$

Rechtsseitiger Grenzwert: $\lim \limits _{x\rightarrow 1^{+}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=0$

Auch diese beiden Grenzwerte stimmen mit dem Funktionswert im Punkt $x=1$ überein: $f(1)=0$

$=>$ Somit ist die Funktion im Punkt $x=1$ stetig.

• $x=0$

Linksseitiger Grenzwert: Ich nähere mich von der negativen x-Achse an den Punkt $x=0$ an:

$\lim \limits _{x\rightarrow 0^{-}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=1$

Rechtsseitiger Grenzwert: Ich nähere mich von der positiven x-Achse an den Punkt $x=0$ an:

$\lim \limits _{x\rightarrow 0^{+}}{(x^{2}-1)\operatorname {sgn}(\sin(\pi x))}=-1$

Der links- und rechtsseitige Grenzwert sind nicht gleich $=>$ Die Funktion ist im Punkt $x=0$ nicht stetig. Warum? Weil die beidseitigen Grenzwerte mit den Funktionswert $f(0)=0$ übereinstimmen müssen, was ja nicht der Fall ist.

---

Die Funktion ist in $\mathbb {R} \backslash (\mathbb {Z} \backslash \{-1,1\})$ stetig.