TU Wien:Diskrete Mathematik für Informatik UE (Gittenberger)/Übungen WS13/Beispiel 1
1) A simple undirected graph is called cubic if each of its vertices has degree 3.
- (a) Find a cubic graph with 6 vertices!
- (b) Is there a cubic graph with an odd number of vertices?
- (c) Prove that for all n ≥ 2 there exists a cubic graph with 2n vertices!
Theory[Bearbeiten | Quelltext bearbeiten]
- Wikipedia: Cubic Graph
- Wikipedia: The Fundamental theorem of arithmetic (s17 Mathematik für Informatik)
- Handshaking lemma (s59 Mathematik für Informatik)
Solution[Bearbeiten | Quelltext bearbeiten]
1.a[Bearbeiten | Quelltext bearbeiten]
1.b[Bearbeiten | Quelltext bearbeiten]
according to the Handshaking lemma
The left side is known to some degree:
as every vertex has a degree of 3
as the number of vertices is an odd number
and
The Fundamental theorem of arithmetic implies that the two sides are not the same and therefore no such graph exists.
( means "Integer n is a divisible by an integer d", see: https://math.stackexchange.com/questions/135253/notation-for-is-divisible-by)
(The should be a "d not divides n")
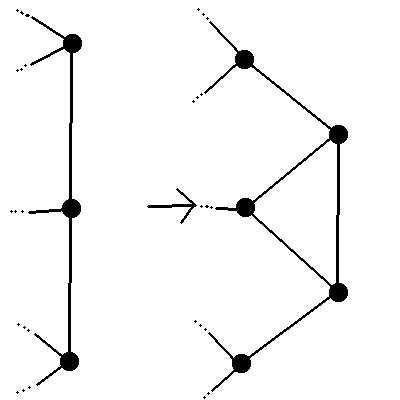
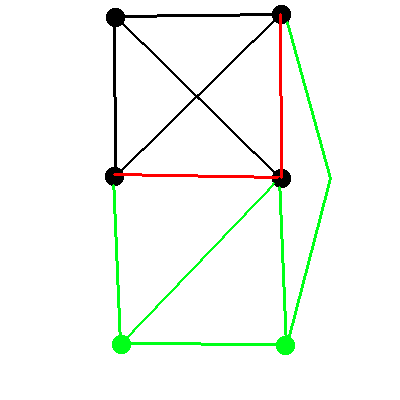
1.c[Bearbeiten | Quelltext bearbeiten]
Proof by induction:
- :
The complete graph with 4-vertices (K4) is a cubic graph.
- :
1. Take a "chain" of 3 vertices
2. Remove the edges connecting them
3. Connect the two new vertices as follows:
e.g :
Formal notation and the proof why the first step is possible are left as an exercise for the reader.