TU Wien:Diskrete Mathematik für Informatik VU (Drmota)/Übungen WS20/Beispiel 4
a) Compute the number of walks of length l from i to j in the graph (see image) by computing powers of its adjacency matrix.
b) How could you use the adjacency matrix to compute the number of triangles (i.e., cycles of length three) in a (loopless) graph? Perform the computation for two graphs of your choice on four vertices.
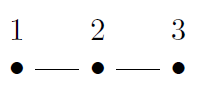
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
a)[Bearbeiten | Quelltext bearbeiten]
The paths of length l can be calculated as the sum of the values in , with A(G) as the adjacency matrix of a graph G
(Walks of length 1: 4)
(Walks of length 2: 6)
(Walks of length 3: 8)
(Walks of length 4: 12)
etc.
b)[Bearbeiten | Quelltext bearbeiten]
Cycles are displayed in the diagonale of a power of an adjacency matrix, in this case .
As each triangle is counted twice for each vertex ("left around" and "right around" in the circle), divide the sum of the values of by .