TU Wien:Einführung in die Mustererkennung VO (Haxhimusa)/Prüfungsausarbeitungen

Einführung in die Mustererkennung Ausarbeitung

Die Fragen hier sind größtenteils aus Informatik-Forums-Threads nach Prüfungen, die konkrete Formulierung bei der Prüfung kann also abweichen.

Kurze Fragen

Design Cycle

• Collect Data
• Choose features (prior knowledge)
• Choose model (prior knowledge)
• Train classifier
• Evaluate classifier

Wenn PCA in der Gesichtserkennung eingesetzt wird heißen die Eigenvektoren oft...

Eigenfaces.

Was versteht man unter Parametrischen- und Nicht-Parametrischen Lernverfahren?

Parametrische Verfahren machen eine Annahme über die Wahrscheinlichkeitsdichte (pdf) z.B: 'Das Merkmal ist Normalverteilt.' Die Parameter der Kurve werden dann geschätzt.

Dadurch ergeben sich folgende Vorteile:

• Es müssen weniger Parameter geschätzt werden, da die Form der Funktion bereits geschätzt wurde
• Somit kann man mit einem kleineren Trainigsset auskommen.

Und ein Nachteil:

• Parametrische Verfahren sind weniger flexibel als Nicht-Parametrische Verfahren.

Nicht-parametrische Verfahren machen keine Annahme über die Wahrscheinlichkeitsdichte (pdf). Hierfür werden so viele Punkte der Wahrscheinlichkeitsdichte (pdf) wie möglich berechnet, der Rest wird interpoliert. Daraus ergibt sich eine Geschätzte Wahrscheinlichkeitsdichte (pdf) die sich für n -> ∞ viele Punkte der tatsächlichen Funktion annähert.

Unter welcher Bedingung konvergiert der Online Perceptron Algorithmus? Was macht dieser Algorithmus wenn diese Bedingung nicht erfüllt ist?

Der Online Perceptron Algorithmus konvergiert nur wenn die beiden Klassen linear separierbar sind. Ist dies nicht der Fall liegt ein XOR-Problem vor und der Algorithmus terminiert nicht. Daher sollte man den Algorithmus nach einer endlichen Anzahl an Iterationen (Epochen genannt) abbrechen.

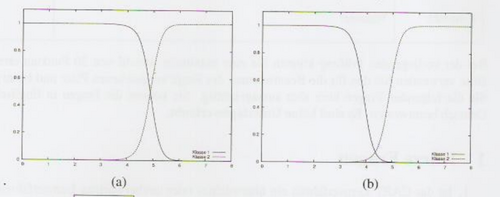
Welche der beiden Kurvenpaare stellt die a posteriori Wahrscheinlichkeiten für ein Klassifikationsproblem mit 2 Klassen dar?

Antwort: (a) Begründung: Alle Wahrscheinlichkeiten addiert muss immer 1 ergeben. Bei (b) zwischen 4 und 5 nicht der Fall

in welche Richtung zeigt der Haupteigenvektor

Der Haupteigenvektor zeigt in Richtung der größten Varianz der Daten.

related: Wikipedia, Hauptkomponentenanalyse

Was versteht man unter einer Euler-Zahl?

Die Euler Zalh (im allgemeinen Kontext eher :Euler-Charakteristik genannt) ist für eine Region definiert als Die Anzahl der Komponenten K minus die Anzahl der Löcher L.

E = K - L

Sie ist verädert sie nicht wenn man die Region streckt und wird darum als Topologisches Merkmal bezeichnet.

Falls σnm = 0 dann sind die Zufallsvariablen...

(a) m und n unabhängig

(b) m und n unkorreliert

Begründung: Unabhängige Variablen => σnm = 0, aber σnm = 0 bedeutet nur, dass die Variablen unkorreliert sind. Über die Unabhängigkeit kann keine Aussage getroffen werden!

Was ist die Syntaktische Mustererkennung?

Syntaktische Mustererkennung versucht im Gegensatz zur Statistischen Mustererkennung nicht Objekte durch Merkmalsvektoren zu beschreiben sondern definiert Primitive und beschreibt Objekte dann als Verhältnisse zwischen diesen Primitiven. Die Regeln nach denen die Primitiven ein Objekt zusammensetzen nennt man Grammatik.

Was ist eine lineare Maschine?

Eine Lineare Maschinen ist beispielsweise eine lineare Diskriminantenfunktion. Sie bildet einen linenaren Klassifikator. Sie wird z.B. in mehrlagigen künstlichen Neuronalen Netzen in den verborgenen Einheiten verwendet. Eine lineare Maschine ist ein Klassifikator der aus einer linearen Diskriminantenfunktion gebildet wird

siehe: Informatik-Forum-Post

Der k-NN Klassifikator ist ein parametrisches oder ein nicht parametrisches Verfahren? Begründung

nicht-parametrisch, da nicht von einer bestimmten Verteilung (zB Normalverteilung) ausgegangen wird. Das Model ist nicht a-priori vorgegeben, sondern wird durch die Daten bestimmt.

Was versteht man unter Parametrischen und nicht-parametrischen Lernverfahren?

Für Parametrische Lernverfahren trifft man am Anfang des Verfahrens eine Annahme über die pdf/Verteilungsfunktion der Daten. Bei Nicht-Parametrischen Lernverfahren ist so eine Annahme nicht notwendig (was allerdings andere Nachteile haben kann).

Wie ist die Varianz der Summe zweier Zufallsvariablen definiert?

Var(X + Y) = Var(X) + Var(Y) + 2Cov(XY)

Falls σmn = 0 dann sind die Zufallsvariablen ...

• (a) m und n unabhängig
• (b) m und n unkorreliert

-> b) Kovarianz = 0 bedeutet dass die Variablen unkorreliert sind. Daraus folgt nicht dass die Variablen auch unabhängig voneinander sind. Umgekehrt ist dies sehr wohl der Fall (unabhängige Variablen sind immer unkorreliert).

Ist k-Means unüberwacht oder überwacht?

K-Means bekommt keine Labelisierten Daten und deshalb unüberwacht.

Welche der folgenden Funktionen können in einem Backpropagation neuronalen Netz als Aktivierungsfunktion verwendet werden?

Sigmoid und tanh

Was versteht man unter „curse of dimensionality“?

Es sollten nicht so viele Merkmale wie möglich verwendet werden, da zusätzliche Merkmale die Leistung eines Klassifikators vermindern können, vorallem wenn die Anzahl der Trainingsbeispiele gering ist. Warum ist das so? z.B.: bei 2 Klassen/10 Trainingsbeispiele (5 pro Klasse)/1 Merkmale vs. 2 Klassen/10 Trainingsbeispiele (5 pro Klasse)/2 Merkmale. Im ersten Fall kann ein Histogramm aufgezeichnet werden, jedes Merkmal ist eindeutig einer Klasse zuzuordnen, im zweiteren Fall gibt es 25 Merkmalkombinationen von denen 15 "unbesetzt", also ohne Trainingswerte bleiben – wie ist die Wahrscheinlichkeit dass dieser Werte (nicht) vorkommen? Wenn doch, wie würden sie klassifiziert werden? Bei 2 Klassen/10 Trainingsbeispiele (5 pro Klasse)/3 Merkmale gibt es schon 125 Kombinationen von denen es für 115 keine Trainingsdaten gibt. Das Verhätnis Stichprobe / Merkmale soll zumindest > 10 sein.

Was versteht man unter „Bias“ und „Varianz“?

Wurde bisher 2x gestellt

Bias

Der Bias eines Klassifikators ist hoch wenn dieser Viele Datenpunkte falsch zuordnet. (underfitting)

Varianz

Die Varianz eines Klassifikators zeigt wie generalisierbar er ist. Wenn die Varianz hoch ist ist die Funktion zwar gut auf die Trainingsdaten angepasst, klassifiziert aber die 'richtigen' Daten (Testset) falsch. (overfitting)

Beides kann mit einem großen Trainingsset niedrig gehalten werden, da man dann einen entsprechend komplexen Klassifikator erstellt.

Welche 2 Arten von Identifizierung in biometrischen Systemen gibt es?

Die Verifizierung und die Erkennung von Personen. Bei der Verifizierung wird zuerst eine Datenbank erstellt die Biometrische Eigenschaften Personen erfasst. Damit kann dann im weiteren die Identität einer Person authentifiziert werden. (z.B. Die Behauptung "Ich bin Herr Huber" untermauert oder widerlegt werden).

Bei der Erkennung geht es um dass ein System in Datensätzen Personen findet, mithilfe einer Datenbank von Personen.

Was ist überwachtes und unüberwachtes Lernen?

Überwachtes Lernen: Für jeden Merkmalsvektor im Trainingsset ist die Klassenzugehörigkeit bekannt (labelisiert).

Unüberwachtes Lernen : Die Klassenzugehörigkeit im Trainingsset ist nicht bekannt, sondern wird im Laufe des Verfahrens anhand der Struktur/Ähnlichkeiten der vorhandenen Daten erlernt.

Anwendungen für unüberwachte Verfahren:

• Labelisierung von Daten kann teuer sein.
• Klassifikatoren die sich selbst an sich ändernde Daten anpassen können.
• Data Mining (knowledge discovery): durch automatische Klassifikation von Daten sollen neue Trends/Merkmale in großen Datenmengen "entdeckt" werden.

Wenn eine Klasse viele Parameter hat, dann ist der Bias ..... und die Varianz ...

Wenn eine Klasse viele Parameter hat, dann ist der Bias niedrig und die Varianz hoch.

Was ist "Gut" an einem Merkmal?

• schnelle/einfache Berechnung / Extraktion
• diskriminativ, d.h. es muss gut zwischen verschiedenen Klassen unterscheiden können.

Was ist syntaktische Mustererkennung?

Objekte werden durch Primitive und deren Verhältnis zueinander beschrieben. Die Erkennung eines Muster durch Finden der Primitive und deren Verhältnis, sowie Analyse der Grammatik/Syntax. D.h. man nimmt an das Muster sei durch Wörter aufgebaut und diese Wörter bestimmen die Klasse des Musters. Siehe z.B. 7-Segment-Anzeige.

2 Blobs und es soll von beiden die Euler Zahl berechnet werden

Anzahl der Komponenten - Anzahl der Löcher

Die Menge aller Punkte für die die Mahalanobis Distanz gleich einer Konstanten c ist, ist durch ein ______________ mit Mittelpunkt ___ gegeben.

Hyperelipsoid, p

Welche der folgenden Funktionen können in einem Backpropagation neuronalen Netz als Aktivierungsfunktion verwendet werden?

• tanh Funktion: $y=\tanh(x)$
• Signum-Funktion: $y=\left\{{\begin{array}{cl}1&{\mbox{wenn }}x>0\\0&{\mbox{wenn }}x=0\\-1&{\mbox{wenn }}x<0\end{array}}\right.$
• sigmoid-Funktion: $y={\dfrac {1}{1+exp\left(-x\right)}}$

Begründung: Es muss sich um eine differenzierbare Funktion handeln, die üblicherweise S-förmig ist.

2 Clustering Algorithmen nennen

K-means, agglomerative und divisive hierarchical Verfahren.

Nennen sie die zwei häufigsten Minutiae.

Unter Minutiae versteht man kleine charakteristische Details eines Fingerabdrucks. Die beiden häufigsten sind:

• Ridge Ending (eine endende Linie)
• Bifurcation (zwei auf einander treffende Linien)

Konvexe Hülle

Die Konvexe Hülle einer Region R ist der durchschnitt aller konvexen Regionen die R umfassen. (Also die Hülle einer Region die keine konkaven Grenzen hat.)

Hamming-Distanz + Anwendungsbeispiel

Die Hamming Distanz ist der "Unterschied" zwischen zwei Zeichenketten, und entspricht der Anzahl unterschiedlicher Stellen. Ein Anwendungsbeispiel dafür ist Iriserkennung. Aus einem Bild von einem Auge wird die Iris extrahiert, und Merkmale werden durch Faltung mit komplex-wertigem 2D Gabor Wavelets mit unterschiedlichen Positionen und Skalierungen berechnet. Diese Merkmale werden in einen 2048Bit (256 Byte) Binärcode umgewandelt. Solche Codes können mithilfe der Hamming Distanz einfach verglichen werden. Achtung: Im Skriptum wird Hamming Distanz / Anzahl der Bits pro Code als Hamming Distanz bezeichnet, während wikipedia die Hamming Distanz als absoluten Wert sieht. Für die im Skriptum definierte "verhältnismäßige" Hamming Distanz gilt: 0 -> identische Codes, 1 -> total unterschiedliche Codes, <= 0.32 -> ausreichend ähnlich.

Detailierte Fragen

Kovarianzmatrix $\Sigma _{j}=I\sigma ^{2}$, beweisen sie dass die Diskriminantenfunktion eine lineare Funktion $g(x)=w^{T}(x-b)$ ist.

In diesem Spezialfall sind die Merkmale innerhalb einer Klasse dekorreliert, weswegen die Kovarianzmatrix $\Sigma _{j}$ nur aus dem Produkt der Identititätsmatrix und der Varianz besteht $I*\sigma ^{2}$. Die Varianz ist für alle Klassen gleich, weswegen die Kovarianzmatrix für alle Klassen gleich ist.

Unter Berücksichtigung der eben genannten Eigenschaften lässt sich die Diskriminantenfunktion, wie folgt, vereinfachen:

$g_{j}(x)=\left(-{\frac {1}{2}}\right)\left({\frac {1}{\sigma ^{2}}}\right)\left(x-\mu _{j}\right)^{T}\left(x-\mu _{j}\right)-{\frac {1}{2}}\ln \left|\Sigma _{j}\right|+\ln \;P\left(\omega _{j}\right)$

$=-{\frac {1}{2\sigma ^{2}}}\left({\cancel {x^{T}x}}\;-\;2\mu _{j}^{T}x\;+\;\mu _{j}^{T}\mu _{j}\right)-{\cancel {{\frac {1}{2}}\ln \left|\Sigma _{j}\right|}}\;+\ln \;P\left(\omega _{j}\right)$

$=-{\frac {1}{2\sigma ^{2}}}\left(\;-\;2\mu _{j}^{T}x\;+\;\mu _{j}^{T}\mu _{j}\right)+\ln \;P\left(\omega _{j}\right)$

Unser Ziel der linearen Diskrimantenfunktion hat die Form $g_{j}(x)=w_{j}^{T}x+w_{j0}$. (Note: Rechenweg aus den Unterlagen. Fragestellung weicht in verlangter Form leicht davon ab.)

Wir können nun aus $g_{j}(x)$ Folgendes extrahieren:

• $w_{j}={\frac {1}{\sigma ^{2}}}\mu _{j}$
• $w_{j0}=-{\frac {1}{2\sigma ^{2}}}\mu _{j}^{T}\mu _{j}+\ln P\left(\omega _{j}\right)$

Diese Terme in die Form der linearen Diskriminantenfunktion eingesetzt, zeigen, dass die Funktion linear ist.

agglomerative hierarchical clustering

beginnen bei n Clustern (gleich die Zahl aller Einzeldaten) und fassen diese Cluster immer weiter zusammen.

Funktion: 1. Am Anfang ist jeder Punkt ein eigener Cluster. 2. Die ähnlichsten zwei Cluster werden gefunden. 3. Diese zwei Cluster werden in einem „Muttercluster“ fusioniert. 4. Schritte 2 und 3 werden wiederholt… bis alle Datenpunkte in einem Cluster sind.

Ergebnis ist ein Dendrogram (Verzweigungsbaum). Ein Vorteil ist, dass man eine Hierarchie bekommt. Um k Gruppen zu bekommen, schneidet man einfach die (k – 1) längste Verbindungen. Es gibt keine echte statistische Begründung für dieses Verfahren

Beschreiben Sie das Complete Linkage Hierachical Clustering Verfahren. Wie funktioniert der Algorithmus? (Geben Sie ein einfaches Beispiel)

SLHC ist ein Agglomeratives Clusteringverfahren bei dem ein Dendogramm erstellt wird. 1) Am Anfang ist jeder Punkt ein Cluster 2) Die ähnlichsten 2 Cluster werden gefunden. (kleinster Abstand - SLC, größter Abstand - Complete LC, mittlerer Abstand - ALC) 3) Diese 2 Cluster werden in einem MutterCluster fusioniert 4) Schritte 2 und 3 werden wiederholt bis alle Datenpunkt in einem Cluster sind oder abgebrochen wird.

Was bedeutet die impurity eines Knotens in in einem Entscheidungsbaum? Warum ist die entropy impurity (Formel) ein geeignetes Maß für die impurity eines Knotens?

Die Impurity eines Knotens in einem Entscheidungsbaum gibt die "Reinheit" des Knotens an. Bei einer impurity von 0, ist der Knoten rein, d.h. alle Muster in einem Knoten gehören zu einer Klasse. Wenn verschiedene Klassen in einem Knoten gleich oft vorkommen, so soll die impurity hoch sein. Ein Ansatz dafür ist die Entropy Impurity:

$i\left(N\right)=-\sum _{j}P\left(w_{j}\right)\log _{2}P\left(w_{j}\right)$

$P\left(w_{j}\right)$ ...Anteil der Muster in Knoten N, die zur Klasse $w_{j}$ gehören. Wert zwischen 0 und 1.

Graph für zwei Werte: Halbkreis. x-Achse: Klasse 1 / 2, y-Achse Impurity. Bei der Entropy Impurity ist der Wert für die Impurity 1 wenn alle Klassen im Knoten gleich oft vorkommen.

Entropy Impurity ist ein geeignetes Maß, da es bei Unreinheit einen hohen Wert annimmt und mit steigender Reinheit kleiner wird. Durch diese Eigenschaft, kann je Knoten ein Wert/Kriterium zum Teilen gefunden werden, bei dem die Impurity Änderung $\Delta i\left(N\right)$ ein Maximum ist.

Sie haben die Klassenwahrscheinlichkeiten $P\left(w_{1}|x\right)$ und $P\left(w_{2}|x\right)$ für ein Problem mit zwei Klassen berechnet, wobei $x$ der Merkmalsvektor ist. Für welche Klasse soll, laut Bayes Decision Rule (Bayer Entscheidungsregel), entschieden werden? Beweisen Sie dass die Bayes-Entscheidungsregel die Fehlerwahrscheinlichkeit $P\left(error\right)$ im Fall von 2 Klassen immer minimiert.

Gegeben die Beobachtung (Merkmalsausprägung) $x=i$, entscheide für die Klasse $k$, welche die größte a posteriori Wahrscheinlichkeit aufweist:

$k=\arg \max _{j}\ P\left(w_{j}|x=i\right)$

Durch diese Entscheidungsregel ergibt sich die bedingte Fehlerwahrscheinlichkeit $P\left(error|x\right)$ zu

$\min[P\left(w_{1}|x\right),P\left(w_{2}|x\right)]=1-\max[P\left(w_{1}|x\right),P\left(w_{2}|x\right)]$

Daher

$P\left(error\right)=\int _{-\infty }^{\infty }P\left(error|x\right)p\left(x\right)dx=\int _{-\infty }^{\infty }\min[P\left(w_{1}|x\right),P\left(w_{2}|x\right)]p\left(x\right)dx$

Die Bayes Rule minimiert also den Integranden $P\left(error|x\right)$ für jede Merkmalsausprägung $x$ und folglich auch die mittlere Fehlerwahrscheinlichkeit.

Wie wird ein Klassifikator als eine Gruppe von Diskriminantenfunktionen dargestellt? Was sind Entscheidungsregionen und Entscheidungsgrenzen? Wie werden diese anhand der Diskriminantenfunktionen definiert? Zeichnen Sie ein 2-Dimensionales Beispiel mit 3-Klassen worin diese Definitionen klar erklärt werden.

Mit jeder Klasse Wi wird eine Funktion gi(x) verbunden.Ein Merkmalsvektor x wird durch die Klasse Wi zugeordnet, wenn gi(x)>gj(x) Vi != j Bei c gegebenen Klassen teilen die Diskriminatnenfunktionen den Merkmalsraum in c Entscheidungsregionen: R1, R2,... Rc Wenn gi(x)>gj(x) Vi != j, dann ist x € Ri und gehört zur Klasse Wi Regionen sind durch Entscheidungsgrenzen getrennt. Die Entscheidungsgrenze zwischen den Klassen W(j) und W(k) ist durch die Gleichung gj(x) =gk(x) gegeben.

Wie wird die Klassifikation anhand der Mahalanobis Distanz durchgeführt? Schreiben Sie den Ausdruck für die Mahalanobis Distanz. Wie werden die Parameter während der Trainingsphase geschätzt? Auf dem Diagramm sind Trainingsvektoren, die zu einer Klasse gehören geplottet. Zeichnen Sie ein paar Konturlinien, die einem konstanten Wert für die Mahalanobis Distanz ab dieser Klasse entsprechen (die Konturlinien sollen ungefähr die richtige Form zeigen, aber müssen nicht genau sein)

Die Mahalanobis Distanz ist ein Distanzmaß zwischen Punkten in einem mehrdimensionalen Vektorraum. Sie ist skalen- und translationsinvariant. Man ordnet das beobachtete Objekt der Gruppe zu, bei der die Distanz des Merkmalvektors x zu dem Erwartungsvektor minimal wird. dj^2(x)=(x−μ)^T E^-1(x- μ) Die Menge aller Punkte für die die Mahalanobis Distanz gleich einer Konstanten c ist, ist durch ein Hyperelipsoid mit Mittelpunkt p gegeben. Der Mahalanobis Distanz Klassifikator bestimmt die kleinste Distanz zu den Clusterzentren

Aufsatz

CART

CART (Classification and Regression Trees) ist ein Algorithmus, der zur Entscheidungsfindung dient. Er wird bei Entscheidungsbäumen eingesetzt.

Der CART-Algorithmus wurde erstmals 1984 von Leo Breiman et al. publiziert [1].

Ein bedeutendes Merkmal des CART-Algorithmus ist, dass nur Binärbäume erzeugt werden können, das heißt, dass an jeder Verzweigung immer genau zwei Äste vorhanden sind. Das zentrale Element dieses Algorithmus ist also das Finden einer optimalen binären Trennung.

Beim CART-Algorithmus wird die Attributsauswahl durch die Maximierung des Informationsgehalts gesteuert. CARTs zeichnen sich dadurch aus, dass sie die Daten in Bezug auf die Klassifikation optimal trennen. Dies wird mit einem Schwellwert erreicht, der zu jedem Attribut gesucht wird. Der Informationsgehalt eines Attributes wird als hoch erachtet, wenn durch die Auswertung der sich aus der Teilung über die Schwellwerte ergebenden Attributausprägungen mit einer hohen Trefferquote eine Klassifikation vorgenommen werden kann. Bei den Entscheidungsbäumen, welche durch den CART-Algorithmus berechnet werden, gilt: Je höher der Informationsgehalt eines Attributs in Bezug auf die Zielgröße, desto weiter oben im Baum findet sich dieses Attribut.

Die Entscheidungsschwellwerte ergeben sich jeweils durch die Optimierung der Spaltenentropie. Die Gesamtentropien der Attribute ergeben sich durch ein gewichtetes Mittel aus den Spaltenentropien.

PCA in der Gesichtserkennung

PCA (Principal Component Analysis) ist ein statistisches Verfahren und dient dazu, umfangreiche Datensätze zu strukturieren, zu vereinfachen und zu veranschaulichen, indem eine Vielzahl statistischer Variablen durch eine geringere Zahl möglichst aussagekräftiger Linearkombinationen (die „Hauptkomponenten“) genähert wird (source).

In der Gesichtserkennung wird die PCA auch verwendet. Dazu werden Aufnahmen von Gesichtern standardisiert (auf gleiche Größe) und in Vektoren gespeichert (aus einem 100 x 100 Pixel Bild wird ein 1 x 10000 Vektor). Mittels der Testdaten wird aus den den Vektoren ein Durchschnittsvektor errechnet und mit diesem "Durchschnittsgesicht" als Referenz können Differenzvektoren zum "Durchschnittsgesicht" berechnet werden. Aus diesen Differenzvektoren können die Kovarianzmatrizen, und in weiterer Folge Eigenvektoren und Eigenwerte berechnet werden. Jeder Eigenvektor hat die selbe Dimension (Anzahl an Komponenten) wie das Ursprungsbild. Diese Eigenvektoren werden Eigenfaces genannt. Diese geben die Richtungen an in welche sie sich vom Durchschnittsvektor unterscheiden.

Zur Gesichtserkennung wird das Gesicht "in Eigenfaces zerlegt", z.B.: ist ein Gesicht das Durchschnittsgesicht + 10% von Eigenface 3, -10% von Eigenface 4 und +3% von Eigenface 8 die Eigenfaces mit der höchsten Ähnlichkeit werden gewählt. 20 - 150 Eigenfaces reichen um Gesichter darstellen zu können. Eine derartige Darstellung eines Gesichts braucht nur sehr wenig Speicher.

(195 wörter)

parametrische / nicht-parametrische Verfahren

Es gibt zwei Möglichkeiten für die Schätzung der pdf (Probability Density Function – Wahrscheinlichkeitsdichtefunktion): Erstens gibt es die nicht-parametrischen Verfahren. Hier wird keine Annahme über die pdf gemacht. Um p(x|ωj) von nj Stichproben der Klasse ωj zu schätzen, wird zunächst eine kürzere Linie mit Zentrum am Punkt x0 erstellt. Diese wird expandiert, bis sie k Stichproben enthält, wobei k vorher festgelegt wird. Vx ist die Länge der Linie, daraus ergibt sich 1/Vx als Schätzung der Dichte. Die Dichte wird für so viele Punkte wie möglich geschätzt, weitere Punkte werden interpoliert. In höheren Dimensionen ist das Verfahren ebenso anwendbar, im zweidimensionalen Fall wird ein Kreis oder Viereck anstatt der Linie verwendet, Vx ist dann die Oberfläche. Die Form der geschätzten Dichtefunktion kann sich sehr mit dem Wert von k ändern. Die geschätzte Dichtefunktion ist normalerweise nicht glatt und nähert sich der echten Funktion, sofern n→∞ geht. Das k-Nearest Neighbour Verfahren basiert darauf, hier wird statt der Likelihood direkt die a posteriori-Wahrscheinlichkeit geschätzt. Die zweite Möglichkeit sind die parametrischen Verfahren, bei denen zu Beginn eine Annahme über die Form der pdf gemacht wird. Hier werden die Parameter der Kurve geschätzt. Vorteile sind hier die geringe Anzahl der zu schätzenden Parameter sowie das Auskommen mit kleineren Trainingssets. Dem gegenüber steht der Nachteil, dass parametrische Verfahren nicht so flexibel sind wie nicht parametrische. Die am häufigsten verwendete Kurve ist die Normalverteilung. Gründe hierfür sind die guten analytischen Eigenschaften. (233 Wörter)

Beschreiben sie den k-means Algorithmus

K-Means ein Algorithmus um einen Datensatz in mehrere Cluster zu Partitionieren. Der Algorithmus funktioniert wie folgt:

• Schritt 0

Die Anzahl der Cluster k wird im vorhinein festgelegt.

z.B.: k = 3

• Schritt 1

Anschließend werden k Cluster-Mittelpunkte zufällig auf dem Datensatz positioniert.

• Schritt 2

Nun wird zu jedem Datenpunkt der nächste Mittelpunkt berechnet.

• Schritt 3

Zu jedem Mittelpunkt wird der Schwerpunkt der in Schritt 2 zugeordneten Datenpunkte berechnet.

• Schritt 4

Der Mittelpunkt wird zu dem Schwerpunkt seiner Datenpunkte verschoben.

• Schritt 5

Wiederhole ab Schritt 2 bis entweder eine festgelegte Iterationstiefe erreicht wird oder sich die Mittelpunkte nicht mehr bewegen. Die Iterationstiefe ist notwendig da der Algorithmus bei einem entsprechenden Datensatz zu Oszilieren beginnen kann.

Rechenbeispiele

PCA

x1= (2 3) x2=(4 5) x3=(6 1)

• a)Berechnen Sie die geschätzte Kovarianzmatrix C.
• b)Berechnen Sie die Eigenwerte dieser Kovarianzmatrix C mit λ1 > λ2

Lösung(!):

• a) C = ({4;-2},{-2;4})
• b) λ1 = 6; λ2 = 2;

Kovarianzmatrix berechnen, Eigenwerte

Eigenwerte: det(Cov - λE) = 0 lösen.. E = Einheitsmatrix

Kovarianzmatrix:

• geschätzen Mittelwert berechnen m = (Summe aller Merkmalsvektoren) * 1 / N
• Kovarianzmatrix: 1 / (N-1) * Summe( (x - m)*(x-m)^T ) // T = transponierter Vektor

Entscheidungsbaum berechnen mit 4 Vektoren, 2 Klassen, 2 Merkmalen und Impurity überall angeben

w1 = weiß w2 = schwarz x1 x2 | x1 x2 0.6 0.18 | 0.09 0.55 0.10 0.44 | 0.15 0.88 (ungefähr so, genau weiß ich nur dass alle weißen von schwarzen getrennt waren mit einer horizontalen Linie) und Bereiche einzeichnen

Siehe Berechnung im Informatik-Forum Entscheidungsbaum berechnen Ich denke mal, dass man sich hier ein paar mühsame Rechnungen erspart indem man die Input-Daten skizziert und optisch die perfekte Schnittgrenze sucht. Dann mit dieser das $\Delta i(N_{root})$ berechnet => oh Wunder es ist maximal (soll heißen gleich $i(N_{root})$ da $\Delta i(N_{root})=i(N_{root})-P_{L}*i(N_{L})-(1-P_{L})*i(N_{R})$ wobei $P_{L}$ und $i(N)$ immer positiv sind)

2 Kurvenpaare, welches stellt a posteriori Wahrscheinlichkeit dar

Bei der a posteriori Wahrscheinlichkeit muss die Summe der beiden Kurven in jedem Punkt 1 ergeben

warum kann man Terme - ln2 Pi - ln p(x) weglassen

Diese Terme sind nicht von wj abhängig und müssen daher beim Vergleich der Diskriminanten Funktionen gj nicht berücksichtigt werden.

Unvollständige / Nicht Textuell beantwortbare Fragen

• Eine geschätzte pdf einzeichnen
• pdf mit Stichproben schätzen
• Haupteigenvektor und zweiten Vektor einzeichnen

Materialien

Neues Material hinzufügen

K

• kurvenpaare.jpg (details)