TU Wien:Funktionale Programmierung VU (Knoop)/Zusammenfassung
Theorie[Bearbeiten | Quelltext bearbeiten]
Typen[Bearbeiten | Quelltext bearbeiten]
Typsynonyme
Typsynonyme (Aliasnamen, Typaliase, ..) erlauben die Semantik von Datentypen durch einen guten sprechenden Namen offenzulegen. Sie verbessern die Lesbarkeit des Codes aber führen keine neuen Typen ein und sorgen somit nicht für erhöhte Typsicherheit. Im unteren Beispiel können sich Kurs und Float gegenseitig vertreten.
type Kurs = Float
type Niedrigst = Kurs
type Hoechst = Kurs
.... usw
-- Erlauben sprechendere Funktionsdefinitionen
auswertung :: Kursausschlag -> Ausschlagsanalyse
auswertung (x,y) = (x,y,geglaettet)
where geglaettet = (4*x+6*y)/10
Neue Typen
Anstatt der Deklaration von Typsynonymen werden neue Typen deklariert:
Konstruktor
|
v
newtype Kurs = K Float
^
|
Typname
newtype Pegelstand = Pgl Float
newtype Koordinate = Koordinate Float -- Typname == Konstruktorname ist erlaubt
--- Der Rest bleibt gleich
newtype Kurs = K Float
type Niedrigst = Kurs
type Hoechst = Kurs
.... usw
-- funktionen jetzt mit Konstruktor
auswertung :: Kursausschlag -> Ausschlagsanalyse
auswertung (K x,K y) = (K x,K y,K geglaettet)
where geglaettet = (4*x+6*y)/10
In diesem Fall sind Niedrigst und Hoechst keine Synonyme mehr für Float, sondern für den neuen Typ Kurs.
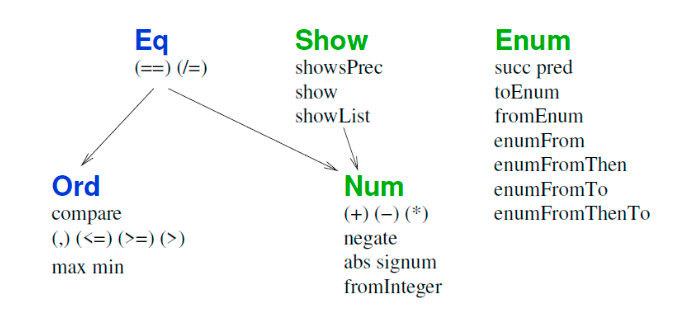
Typklassen
Typklassen haben Typen als Elemente und legen Menge von Operationen und Relationen fest, die auf Werten ihrer Elemente implementiert werden müssen. Sie können vollständige Standardimplementierungen oder noch zu vervollständigende Protoimplementierungen vorsehen. Typen werden durch Instanzbildung zu Elementen (= Instanzen) einer Typklasse.
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x==y) -- Protoimplementierungen
x == y = not (x/=y) -- für (/=) und (==)
---- Instanzbildung
instance Eq Bool where
True == True = True
False == False = True
_ == _ = False
-- weil (==) und (/=) sich aufeinander abstützen reicht Implementierung der einen
instance Eq Kurs where
K k1 == K k2 = k1 == k2
instance Ord Kurs where
K k1 <= K k2 = k1 <= k2
Man spricht von Überladung wenn es mehrere Funktionen mit dem gleichen Namen gibt und der Typ der Argumente bestimmt welche von ihnen gemeint ist.
-- direkt überladen weil unmittelbar in Typklasse eingeführt
(==) :: Eq a => a -> a -> Bool
(>=) :: Ord a => a -> a -> Bool
betrag_in_Muenzen_verschieden_zahlbar :: Waehrung a => a -> Int
-- indirekt überladen weil zwar nicht selbst in Typklasse eingeführt aber auf solche Funktionen abgestützt
f :: (Num a, Waehrung a) => a -> a -> a
f a b = .. betrag_in_Muenzen_verschieden_zahlbar ..
-- nicht überladene Funktionen haben leeren Signaturkontext
fac :: Integer -> Integer
first :: (a,b) -> a
length :: [a] -> Int
Algebraische Datentypen
data Deklarationen zur Definition originär neuer Typen auf drei Arten:
Aufzählungstypen - 0-stelliger Konstruktor, Typen mit endlich vielen Werten
data Geschlecht = Männlich | Weiblich -- vordefinierte Aufzählungstypen data Ordering = LT | EQ | GT deriving (Eq, Ord, Bounded, Enum, Read, Show)
Produkttypen - mehrstelliger Konstruktor, möglicherweise unendlich viele Werte
data Person = P Vorname Nachname -- (echter Produkttyp) data Person = P (Vorname, Nachname, Geschlecht) -- (unechter Produkttyp)
Summentypen - Mindestens zwei Konstruktoren von denen einer nicht 0-stellig ist, Typen mit Werten, die sich aus der Vereinigung der Werte verschiedener Typen mit jeweils möglicherweise unendlich vielen Werten ergeben
data Baum = Blatt Int | Wurzel Baum Int Baum -- rekursiver Summmentyp
Rekursion und Rekursionstypen[Bearbeiten | Quelltext bearbeiten]
Repetitive/schlichte/einfache Rekursion:
pro Zweig maximal ein rekursiver Aufruf und stets als äußerste Operation
ggt :: Int -> Int -> Int
ggt m n
| n == 0 = m
| m >= n = ggt (m-n) n
| m < n = ggt (n-m) m
Lineare Rekursion
pro Zweig maximal ein rekursiver Aufruf und mindestens einer nicht als äußerste Operation
powerThree :: Int -> Int
powerThree n
| n == 0 = 1
| n > 0 = 3 * powerThree (n-1)
^
|
äußerste Operation!
Baumartige Rekursion pro Zweig mehrere weitere Aufrufe (Baum)
binom :: Int -> Int -> Int
binom n k
| k == 0 || n == k = 1
| otherwise = binom (n-1) (k-1) + binom (n-1) k
Geschachtelte Rekursion
rekursive Aufrufe haben rekursive Aufrufe als Argument
fun91 :: Int -> Int
fun91 n
| n > 100 = n - 10
| n <= 100 = fun91 (fun91 (n+11))
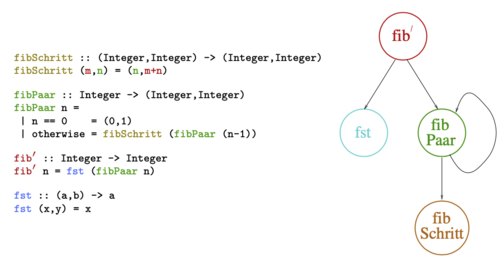
Aufrufgraphen
Der Aufrufgraph eines Systems von Rechenvorschriften namens ist ein Graph, der
- für jede in deklarierte Rechenvorschrift einen Knoten mit dem Namen der Vorschrift als Beschriftung enthält
- eine gerichtete Kante vom Knoten zu Knoten genau dann enthält, wenn im Rumpf der zu gehörigen Rechenvorschrift die zu gehörige Rechenvorschrift aufgerufen wird.
Was lässt sich anhand von Aufrufgraphen erkennen?
- Direkte Rekursion - Selbstkringel, siehe
fibPaar - Wechselweise Rekursivität - Siehe
isOddundisEven
- Direkte hierarchische Abstützung - es gibt eine Kante in eine Richtung von einem Knoten zu einem anderen
- Indirekte hierarchische Abstützung - Knoten ist über andere Knoten erreichbar, nur in eine Richtung
- Indirekte wechselweise Abstützung - Knoten ist über Folge von Kanten erreichbar, und umgekehrt
- Unabhängigkeit/Isolation - Knoten hat weder ein- noch ausgehende Kanten (ausser evtl. Selbstkringel)
Auswertung von Ausdrücken[Bearbeiten | Quelltext bearbeiten]
Ziel ist es, Ausdrücke soweit zu vereinfachen wie möglich und so ihren Wert zu berechnen.
Dafür müssen zwei Arten von Schritte zusammenspielen:
Expandieren (E) - Funktionsterme, Funktionsaufrufe
simple :: Int -> Int -> Int -> Int simple x y z = (x + z) * (y + z) --- simple 2 3 4 (E) ->> (2+4) * (3+4)
Simplifizieren (S) - Funktionstermfreie Ausdrücke
(S) ->> 6 * (3+4) (S) ->> 6 * 7 (S) ->> 42
Hauptauswertungsreihenfolgen für natSum
natSum n = if n == 0 then 0 else natSum (n-1) + n
Applikativ (eager, early) - Zuerst Argument auswerten, dann Funktion ausführen[Bearbeiten | Quelltext bearbeiten]
Vor der Expansion gilt: Jedes Argument wird genau ein Mal ausgewertet
Ein Funktionsterm wird ausgewertet indem:
- die Argumentausdrücke vollständig zu ihren Werten ausgewertet werden
- werden im Rumpf von als Parameter eingesetzt
- der entstandene expandierte Ausdruck wird ausgewertet
natSum 3
(E) ->> if 3 == 0 then 0 else natSum (3-1) + 3
(S) ->> if False then 0 else natSum (3-1) + 3
(S) ->> natSum (3-1) + 3
(S) ->> natSum 2 + 3
(E) ->> (if 2 == 0 then 0 else natSum (2-1) + 2) + 3
(S) ->> (if False then 0 else natSum (2-1) + 2) + 3
(S) ->> (natSum (2-1) + 2) + 3
(S) ->> (natSum 1 + 2) + 3
(E) ->> ...
... (S) ->> 6
Normal - Funktion mit unausgewerteten Parametern ausführen, dann Parameter auswerten[Bearbeiten | Quelltext bearbeiten]
Ein Funktionsterm wird ausgewertet indem:
- die Argumentausdrücke werden unausgewertet im Rumpf von als Parameter eingesetzt
- der entstandene expandierte Ausdruck wird ausgewertet
Vor der Expansion gilt: Jedes Argument wird so oft ausgewertet wie nötig
natSum 3
(E) ->> if 3 == 0 then 0 else natSum (3-1) + 3
(S) ->> if False then 0 else natSum (3-1) + 3
(S) ->> natSum (3-1) + 3
(E) ->> (if (3-1) == 0 then 0 else natSum ((3-1)-1) + (3-1)) + 3
(S) ->> (if 2 == 0 then 0 else natSum ((3-1)-1) + (3-1)) + 3
(S) ->> (if False then 0 else natSum ((3-1)-1) + (3-1)) + 3
(S) ->> natSum ((3-1)-1) + (3-1) + 3
(E) ->> (if ((3-1)-1) == 0 then 0 else ... ) + (3-1) + 3
... (S) ->> 6
Linksapplikativ oder Linksnormal[Bearbeiten | Quelltext bearbeiten]
Applikative oder normale Auswertung beantwortet die Frage Wie ist mit Argumenten umzugehen? bzw. Argumente ausgewertet (applikativ) oder unausgewertet (normal) übergeben?.
Linksapplikativ bzw. Linksnormal ist die Antwort auf die Frage Wo ist im Ausdruck auszuwerten?
Linksapplikative und linksnormale Auswertung können sich im Terminierungsverhalten unterscheiden. Wohingegen die applikative Auswertung nicht terminiert und somit das Resultat undefiniert ist, terminiert die normale Auswertung.
Auch die Terminierungsgeschwindigkeit unterscheidet sich
jedoch ist bei Terminierung das Ergebnis immer gleich (Diamond Property).
Vergleich der Auswertungsordnungen
Normale Auswertung - Argumente so oft wie sie verwendet werden auswerten
(+) Kein unbenötigtes Argument wird ausgewertet
(+) Terminiert immer wenn es eine terminierende Auswertung gibt
(-) Argumente die mehrfach verwendet werden, werden mehrfach ausgewertet
Frühe, fleißige applikative Auswertung - Argumente werden genau ein Mal ausgewertet
(+) Jedes Argument wird exakt ein Mal ausgewertet
(-) Auch nicht benötigte Argumente werden ausgewertet
Späte, faule Auswertung - Argumente werden höchstens ein Mal ausgewertet
(+) Argument nur ausgewertet wenn benötigt
(+) Kombination aus applikativer (Effizienz) und normaler (Terminierung) Auswertung
(-) Zusätzlicher Zeitaufwand zur Verwaltung der Auswertung von Teilausdrücken
Polymorphie[Bearbeiten | Quelltext bearbeiten]
Polymorphe Datentypen
Ein algebraischer Typ, neuer Typ oder Typsynonym heißt polymorph, wenn einer oder mehrere Grundtypen der Werte von in Form einer oder mehrerer Typvariablen als Typparameter angegeben werden.
-- polymorpher algebraischer Datentyp
data Baum a b c = Blatt a b | Wurzel (Baum a b c) c (Baum a b c)
data Liste a = Leer | Kopf a (Liste a)
data Eq a => Liste' a = Leer' | Kopf' a (Liste' a) -- Kontexteinschränkung erlaubt
-- polymorpher neuer Typ
newtype Triplepaar a b c d = Tp ((a,b,c), (b,c,d))
newtype Paar a = P (a,a)
newtype Ord a => Paar' a = P' (a,a) -- Kontexteinschränkung erlaubt
-- Typsynonyme
type Assoziationssequenz a b = [(a,b)]
-- Kontexteinschränkung nicht erlaubt!
Parametrische Polymorphie auf Funktionen
Eine Funktion heißt parametrisch (echt) polymorph, wenn die Typen eines oder mehrerer ihrer Parameter angegeben durch Typvariablen Werte beliebiger Typen als Argument zulassen. Erkennbar daran, dass keine Typvariable typkontexteingeschränkt ist.
id :: a -> a
id x = x
curry :: ((a,b) -> c) -> (a -> b -> c)
curry f x y = f (x,y)
Ad-Hoc Polymorphie auf Funktionen
Eine schwächere, weniger generelle Form der Polymorphie, daher auch unechte Polymorphie oder Überladung genannt. Eine Funktion ist ad hoc polymorph wenn die Typen eines oder mehrerer ihrer Parameter durch Typkontexte eingeschränkt sind.
-- direkt überladen weil in vordefinierter Typklasse angegeben
(+) :: Num a => a -> a -> a
(==) :: Eq a => a -> a -> Bool
(>) :: Ord a => a -> a -> Bool
-- indirekt überladen, stützen sich auf überladene Funktion ab ohne selbst in Typklasse eingeführt zu sein
sum :: Num a => [a] -> a
sum [] = 0
sum (x:xs) = x + sum xs
^
|
(+) direkt überladen
Ad hoc vs. parametrische Polymorphie
Wiederverwendung durch ad hoc Polymorphie bedeutet die Widerverwendung des Funktionsnamens jedoch nicht der Funktionsimplementierung! Diese muss typspezifisch bei der Typklasseninstanzbildung ausprogrammiert werden.
Beispiel aus dem Semester damit ich (+) mit Zahlraum_0_10 nutzen kann:
data Zahlraum_0_10 = N | I | II | III | IV | V | VI
| VII | VIII | IX | X | F deriving (Eq,Ord,Show,Enum)
instance Num Zahlraum_0_10 where
(+) n1 n2
| n1 == F || n2 == F || ((fromEnum n1) + (fromEnum n2)) > 10 = F
| otherwise = toEnum ((fromEnum n1) + (fromEnum n2))
... usw
Wohingegen paramterische Polymorphie die Wiederverwendung von Funktionsnamen und Funktionsimplementierung erlaubt. Intuitiv kann ich map, foldr, foldl, usw auf alle Arten von Listen anwenden egal ob [Char] oder [Int].
Error Handling[Bearbeiten | Quelltext bearbeiten]
Panikmodus
Fehler sowie Fehlerursache werden gemeldet und die fehlerhafte Programmauswertung wird gestoppt.
error :: String -> a
Vorteile: Generell, einfach, schnell und stets anwendbar
Nachteile: Radikal, das heißt die Berechnung stoppt unwiderruflich und jegliche Information über den Programmablauf ist verloren. Für sicherheitskritische Systeme unter Umständen fatal.
Auffangwerte
Um den Panikmodus zu vermeiden und den Programmlauf nicht komplett abzubrechen können funktionsspezifische oder aufrufspezifische Auffangwerte zur Weiterrechnung im Fehlerfall geliefert werden.
Funktionsspezifischer Auffangwert
fac :: Integer -> Integer
fac n
| n == 0 = 1
| n > 0 = n * fac (n-1)
| otherwise = -1
Nachteil hier ist jedoch, dass das Eintreten der Fehlersituation verschleiert wird und somit intransparent gemacht wird wenn der Auffangwert auch als Resultat einer regulären Berechnung auftreten kann. Es ist auch oft nicht leicht einen plausiblen Wert als Auffangwert zu bestimmen, oder es fehlt gänzlich einer.
Aufrufspezifischer Auffangwert
fac :: Integer -> Integer
fac n
| n == 0 = 1
| n > 0 = n * fac (n-1)
| otherwise = n
Flexibel und generell da variierende Fehlerwerte bzw. Fehlerbehandlung möglich ist. Jedoch wie oben nicht transparent und die Gefahr der ausbleibenden Fehlerwahrnehmung.
Fehlertypen, Fehlerwerte, Fehlerfunktionen
Das Ziel ist das systematische Erkennen, Anzeigen und Behandeln von Fehlersituationen. Dafür werden dezidierte Fehlertypen, Fehlerwerte und Fehlerfunktionen genutzt anstatt schlichter Auffangwerte.
In Haskell der Fehlerdatentyp Maybe
data Maybe a = Just a | Nothing deriving (Eq, Ord, Read, Show)
Beispielhaft in der Division:
div' :: Int -> Int -> Maybe Int
div' n m
| m /= 0 = Just (div n m)
| m == 0 = Nothing
---
div' 13 5 ->> Just 2 -- division geklappt
div' 13 0 ->> Nothing -- nope
Fehler können erkannt, angezeigt, weitergereicht und als Auffangwerte behandelt werden. Jedoch ist die Funktionalität geändert worden mit Maybe b anstatt b.
Probetest[Bearbeiten | Quelltext bearbeiten]
Ausgearbeitete Fragen alter Probetests
Welches ist die Standardauswertung von Haskell?
Lazy Evaluation - effiziente Implementierungsumsetzung linksnormaler Auswertung bei der Ergebnisse auszuwertender Ausdrücke nur so weit wie benötigt berechnet werden.
Was versteht man unter einem Operatorabschnitt?
Partiell ausgewertete Binäroperatoren wie z.B.: (*2) dbl - eine Funktion die ihr Argument verdoppelt
Was ist mit Funktionen als first class citizens in funktionalen Programmiersprachen gemeint?
Ausdrücke mit funktionalen Wert dürfen praktisch überall dort stehen, wo auch Ausdrücke mit elementarem Wert stehen (und umgekehrt). Das bedeutet Funktionen können auch anderen Funktionen als Argument übergeben werden oder als Wert retourniert werden.
Definiere einen Operator ; für die Hintereinanderausführung von Funktionen von links nach rechts inklusive Signatur
(;) :: (a -> a) -> (a -> a) -> a -> a
((;) g f) x = f (g x)
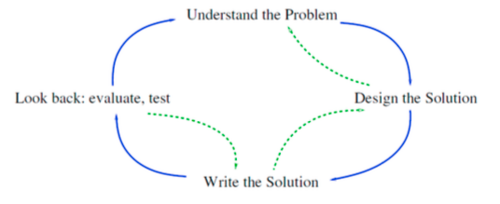
Was versteht Simon Thompson unter reflektivem Programmieren?
Understand the problem, design the solution, write the solution, look back, evaluate and test. Programmentwicklung mit Rückkopplungsschleifen.
Was kann in Haskell polymorph deklariert werden?
- Funktionen: Parametrische (echte) Polymorphie (
map) oder ad hoc Polymorphie (+, direkt überladen bzw.sumindirekt überladen )
- Datentypen: Algebraische Datentypen mit
data, Neue Typen mitnewtype, Typsynonyme mittype
Was ist mit der record-Syntax in Haskell gemeint?
Produkt- bzw. Verbundtypen mit möglicherweise unendlich vielen (Tupel-) Werten
data Meldedate = Md { vorname :: String,
nachname :: String,
geboren :: Gb,
strasse :: String,
hausnummer :: Int
} deriving (Eq, Ord, Show)
Welchen Typ hat das vordefinierte Funktional map auf Listen in Haskell?
map :: (a -> b) -> [a] -> [b]
Geben Sie zwei unterschiedliche Implementierungen für map an
map' :: (a -> b) -> [a] -> [b]
map' f ls = [ f x | x <- ls]
------------------------------
map'' :: (a -> b) -> [a] -> [b]
map'' f [] = []
map'' f (ls:s) = f ls : map'' f s
Was sind Muster in Haskell und wozu sind sie nützlich?
Syntaktische Ausdrücke, die die Struktur von Werten beschreiben. Mittels pattern matching können in der Funktionsdefinition durch Muster festgelegte Alternativen ausgewählt werden. Sind nützlich weil elegant und knoop, gut lesbar können aber auch zu subtilen Fehlern führen.
sortiere :: [Integer] -> [Integer]
sortiere [] = [] -- Muster leere Liste
sortiere (n:[]) = [n] -- Muster einelementige Liste
sortiere (n:ns) = .... -- Muster Liste Länge 2+
Wie sind Typklassen in Haskell aufgebaut? Wozu dienen Sie und mit welcher Art von Polymorphie sind sie eng verbunden?
Hierarchischer Aufbau, sind Konstrukt der funktionalen Programierung zur Implementierung von Ad hoc Polymorphie.
Was ermöglicht Ad hoc Polymorphie wiederzuverwenden?
Ad hoc Polymorphie (auch unecht, überladen genannt) unterstützt die Wiederverwendung des Funktionsnamens aber nicht der Funktionsimplementierung. Die Implementierung wird typspezifisch bei der Typklasseninstanzbildung ausprogrammiert.
Implementieren Sie die Funktion f bedeutungsgleich mithilfe bewachter Ausdrücke, argumentfrei mithilfe anonymer Lambda Abstraktion und mithilfe einer Listenkomprehension
f :: Integer -> Integer
f n = if n == 0 then 0 else f (n-1) + n * n
------------------------------------------
f' :: Integer -> Integer
f' n
| n == 0 = 0
| otherwise = f (n-1) + n*n
------------------------------------------
f'' :: Integer -> Integer
f'' = \n -> (if n == 0 then 0 else f'' (n-1) + n * n)
------------------------------------------
f''' :: Integer -> Integer
f''' n = sum [ x*x | x <- [0..n]]
Geben Sie möglichst typallgemeine Definition für Bäume und Wälder in Haskell an.
data Baum a b c = Blatt a | Knoten b c [Baum a b c]
type Wald a b c = [Baum a b c]
Machen Sie den Baumtyp zu einer Instanz der Typklasse Eq (ohne deriving Klausel).
instance (Eq a,Eq b,Eq c) => Eq (Baum a b c) where
(Blatt x) == (Blatt y) = x == y
(Knoten y1 z1 baum1) == (Knoten y2 z2 baum2) = y1 == y2 && z1 == z2 && baum1 == baum2
_ == _ = False
Was bedeutet die folgende Signatur in curryfizierter und uncurryfizierter Lesart?
h :: (a -> b) -> [a] -> [b]
curryfiziert:
hbildet eine Funktion vom Typ(a -> b)auf eine Funktion vom Typ([a] -> [b])ab. Entspricht somit(a -> b) -> ([a] -> [b])curry macht man mit vielen zutaten die man nacheinander reingibt
uncurryfiziert :
hbildet ein Argument vom Typ[a]auf einen Wert vom Typ[b]mithilfe einer Funktion vom Typ(a -> b)ab.
SETs[Bearbeiten | Quelltext bearbeiten]
Ausgearbeitete Fragen der SETs
Was ist der Unterschied zwischen Wertvereinbarungen in funktionalen Sprachen und Wertzuweisungen in imperativen SPrachen?
Am einfachsten darzustellen mittels selbstbezüglicher Wertzuweisungen wie
x = x + 1
Interpretiert als Wertzuweisung wird in die mit x bezeichnete Speicherzelle der dort gespeicherte Wert um 1 erhöht.
Interpretiert als Wertvereinbarung ist die Bedeutung undefiniert! Es gibt keinen Wert der x für diese Gleichung erfüllt, dementsprechend endet eine solche Zuweisung im Stack Overflow.
type, newtype und data sind untereinander austauschbar, wahr oder falsch?
Falsch, weil:
typeführt lediglich Typsynonyme bzw. Aliasnamen ein für Typen die bereits definiert sind.type Niedrigst = Kurs type Hoechst = Kurs
newtypeverleiht Werten eines existierenden Typs eine neue Identität. Werte des bisherigen Typs werden zu Argumenten des Konstruktors des neuen Typs. Neue Typen einzuführen ist mitnewtypemöglich aber eingeschränkt.newtype Kurs = K Float ^ | Konstruktor
dataDeklarationen erlauben uneingeschränkt neue Datentypen einzuführen. JedenewtypeDeklaration kann durch einedataDeklaration ersetzt werden, aber nicht umgekehrt!data Jahreszeiten = Fruehling | Sommer | Herbst | Winter data Person = P Vorname Nachname Geschlecht
Worin unterscheiden sich echte und unechte Polymorphie?
Echt polymorphe Funktionen haben genau eine Implementierung die für alle konkreten Typen funktioniert die für die Typvariablen in der Signatur eingesetzt werden. Unecht polymorphe Funktionen haben für jeden Typ auf dessen Werten sie arbeiten können eine eigene typspezifische Implementierung
(==) :: Eq a => a -> a -> Bool
Woran erkennt man Funktionen erster bzw. höherer Ordnung?
Eine Funktion erster Ordnung besitzt als Argumente und Resultat nur Elementarwerte wohingegen eine Funktion höherer Ordnung Funktionen als Argumente und/oder als Resultat besitzt.
Curryfizierte und uncurryfizierte lesart von uncurry
uncurry :: (a -> b -> c) -> (a,b) -> c
Curryfiziert - uncurry ist eine 1-stellige Funktion, die Funktionen, die a-Werte auf Funktionen abbildet, die b-Werte auf c-Werte abbilden, auf Funktionen abbildet, die Paare von a- und b-Werten auf c-Werte abbilden.
Uncurryfiziert - uncurry ist eine 2-stellige Funktion, die Funktionen, die a-Werte auf Funktionen abbildet, die b-Werte auf c-Werte abbilden, und Paare von a- und b-Werten auf c-Werte abbildet.
Welche Varianten algebraischer Datentypen lassen sich unterscheiden?
- Produkttypen (echt/unecht)
data Person = P Vorname Nachname Geschlecht -- (echter Produkttyp)
data Person = P (Vorname,Nachname,Geschlecht) -- (unechter Produkttyp)
Summentyp: Mindestens zwei Konstruktoren, mindestens ein nicht nullstelliger Kon- struktor, z.B.
data Baum = Blatt Int | Wurzel Baum Int Baum
Merkregel
data SumType = S1 Int | S2 Char
data ProdType = P Int Char
-- Mögliche Werte --
|SumType| = |Int| + |Char|
|ProdType| = |Int| * |Char|
Der Multiplikationsoperator (*) bezeichnet in Haskell eine Funktion höherer Ordnung, wahr oder falsch?
Wahr - der Multiplikationsoperator ist curryfiziert angegeben als 1-stellige Funktion auf a-Werten als Definitionsbereich mit der Menge der 1-stelligen Funktionen auf a-Werten als Bildbereich. Somit ist der Operator eine Funktion höherer Ordnung, da er angewendet auf ein Argument eine Funktion liefert z.B.:
Prelude> mal3 = (*3)
Prelude> mal3 4
12
Geben Sie je eine beliebige, aber korrekte Implementierung für f und g an
f :: (a -> b) -> [a] -> [b]
f fkt ls = [fkt x | x <- ls]
g :: a -> b -> [a] -> [b]
g x y [] = []
g x y (z:zs) = if x == z then y : (g x y zs) else g x y zs
Welchen Typ hat foldr? Leiten Sie aus der Implementierung den allgemeinstmöglichen Typ her.
foldr f e [] = e
foldr f e (l:ls) = f l (foldr f e ls)
-- e ist "Basiswert"
foldr :: (a -> b -> b) -> b -> [a] -> b
Mit welchen Werten für f und e muss foldr aufgerufen damit Konjunktion/Disjunktion einer Liste von Bools berechnet wird?
ww = [True,True,False,False,True]
konjunktion = foldr (&&) True ww
disjunktion = foldr (||) False ww
Was sind Operatorabschnitte in Haskell?
Partiell ausgewertete Binäroperatoren wie z.B.: (*2) dbl - eine Funktion die ihr Argument verdoppelt. Siehe auch mal3 2 = 6.
Werten Sie die gegebene Funktion kubik 3linksnormal bzw. linksapplikativ aus
kubik :: Int -> Int
kubik 1 = 1
kubik n = n^3 + kubik (n-1)
Linksnormal:
(E) 3^3 + kubik (3-1)
(S) 27 + kubik (3-1)
(E) 27 + (3-1)^3 + kubik ((3-1)-1)
(S) 27 + (2^3) + kubik ((3-1)-1)
(S) 27 + 8 + kubik ((3-1)-1)
(S) 35 + kubik ((3-1)-1)
(E) 35 + 1
(S) 36
Linksapplikativ:
(E) 3^3 + kubik (3-1)
(S) 27 + kubik (3-1)
(S) 27 + kubik 2
(E) 27 + (2^3) + kubik(2-1)
(S) 27 + 8 + kubik(2-1)
(S) 35 + kubik(2-1)
(S) 35 + kubik 1
(E) 35 + 1
(S) 36
Implementieren Sie map :: (a -> b) -> [a] -> [b]:
- rekursiv
mapR :: (a -> b) -> [a] -> [b]
mapR f [] = []
mapR f (x:xs) = (f x) : mapR f xs
- mit Listenkomprehension
mapL :: (a -> b) -> [a] -> [b]
mapL f ls = [f x | x <- ls]
- argumentfrei mit Lambda
mapLambda :: (a -> b) -> [a] -> [b]
mapL = \f xs -> [f x | x <- xs]
Jede Implementierung von f ist auch eine Implementierung von g und umgekehrt
f :: a -> b -> ([a] -> [b])
g :: a -> b -> [a] -> [b]
Ja, da in Haskell Typsignaturen implizit rechtsassoziativ geklammert sind, sind die Signaturen von f und g gleichbedeutend. Offensichtlich wenn vollständig (aber NiChT ÜbErFlÜsSiG) geklammert.
f :: (a -> (b -> ([a] -> [b])))
g :: (a -> (b -> ([a] -> [b])))
In einer voll ausgebildeten funktionalen Sprache wie Haskell ist rein applikative Programmierung fast nicht möglich
Richtig da die arithmetischen Grundoperationen in Haskell curryfiziert vordefiniert und deshalb Funktionen höherer Ordnung sind. Nach Konsumation des ersten Arguments liefern sie eine Funktion als Resultat (siehe Operatorabschnitte).
Normale und applikative Auswertung führen stets zum selben Ergebnis
Jein, sie unterscheiden sich nicht nur in Dauer sondern auch im Terminierungsverhalten. Insofern beide terminieren führen sie aber zum selben Ergebnis (Diamond Property).
Was ist im jeweils strengen Sinn mit applikativer und funktionaler Programmierung gemeint?
Applikativ - Funktionen werden ausschließlich auf elementare Werte angewendet und liefern ausschließlich elementare Resultate zurück
Funktional - Funktionen werden ausschließlich auf funktionale Werte angewendet und liefern ausschließlich funktionale Resultate
In der Praxis gibt es weder das eine noch das andere in reiner Form
Was sind direkt überladene Funktionen?
Funktionen die in einer der Typklassen eingeführt sind, heißen direkt überladen oder unecht polymorph. Beispiele sind die Operatoren (==) und (/=) aus der Typklasse Eq.
Auswertungsreihenfolgen
type Nat0 = Integer
type Nat1 = Integer
fib :: Nat0 -> Nat0
fib n = if n == 0 || n == 1 then n else fib (n-1) + fib (n-2)
hoch :: Nat0 -> Nat0 -> Nat1
hoch m n = if n == 0 then 1 else m * hoch m (n-1)
-- linksapplikativ
->> 42 * (hoch (2*3) (fib (17+4))) + 21 - (hoch 47 11) + (fib (hoch (2+3) (fib (21*2))))
(S) 42 * (hoch (6) (fib (17+4))) + 21 - (hoch 47 11) + (fib (hoch (2+3) (fib (21*2))))
(S) 42 * (hoch 8 (fib 21)) + 21 - (hoch 47 11) + (fib (hoch (2+3) (fib (21*2))))
-- rechtsnormal lol
->> 42 * (hoch (2*3) (fib (17+4))) + 21 - (hoch 47 11) + (fib (hoch (2+3) (fib (21*2))))
(E) 42 * (hoch (2*3) (fib (17+4))) + 21 - (hoch 47 11) +
(if (hoch (2+3) (fib (21*2)) == 0 || (hoch (2+3) (fib (21*2)) == 1
then hoch (hoch (2+3) (fib (21*2))
else fib((hoch (2+3) (fib (21*2))-1) + fib((hoch (2+3) (fib(21*2))-2))
(E) 42 * (hoch (2*3) (fib (17+4))) + 21 - (hoch 47 11) +
(if (hoch (2+3) (fib (21*2)) == 0 || (if (2+3) == 0 then 1 else (fib (21*2) * hoch fib(21*2) (2+3)-1) == 1
then hoch (hoch (2+3) (fib (21*2))
else fib((hoch (2+3) (fib (21*2))-1) + fib((hoch (2+3) (fib(21*2))-2))
Was spricht für eager evaluation und was für lazy evaluation in Programmiersprachen? Was dagegen?
Eager - Einfachere Implementierung, schnellere Terminierung und die in der Mathematik bevorzugte Sicht, dass aus der Undefiniertheit eines Funktionsarguments auch die Undefiniertheit des Funktionswerts folgen soll. Funktionen werden exakt einmal ausgewertet, aber auch dann wenn ihr Wert nicht benötigt wird.
Lazy - Auswertung terminiert definitiv wenn es nur irgendeine Auswertungsreihenfolge gibt, für die das zutrifft. Auswertung findet auch nur statt wenn Werte benötigt werden.
Nachteile sind die technisch anspruchsvollere Implementierung. Lazy evaluation vereint durch Ausdrucksteilung die Vorteile applikativer Auswertung (Effizienz) und normaler Auswertung (Terminierungshäufigkeit).
Was ist die Bedeutung der drei Reduktionsregeln im Lambdakalkül?
- -Reduktion zur gebundenen Umbenennung von Funktionsparametern
- -Reduktion zur Funktionsanwendung
- -Reduktion zur Elimination unnötiger Funktionen
Was ist die Bedeutung eines Lambdaausdrucks?
Die Bedeutung von Lambdaausdrücken ist ihre Normalform, wenn sie existiert. Die Eindeutigkeit der Normalform ist garantiert, wenn sie existiert.
Operatorabschnitte können in Haskell mit jedem Operator gebildet werden
Falsch, nur mit zweistelligen Operatoren.
Die Auswertung von Haskell-Programmen ist immer lazy
Falsch, standard ist zwar lazy aber kann mithilfe ($!) eine eager evaluation erzwungen werden.
Klammerung
Seien folgende Deklarationen gegeben:
type Nat0 = Integer
type Nat1 = Integer
fib :: Nat0 -> Nat0
fib n = if n == 0 || n == 1 then n else fib (n-1) + fib (n-2)
hoch :: Nat0 -> Nat0 -> Nat1
hoch m n = if n == 0 then 1 else m * hoch m (n-1)
sowie
42 * (hoch (2*3) (fib 17+4)) + 21 - (hoch 47 11 * 3) - fib (hoch (2+3) (fib 21) * 2)
vollständig (aber nicht überflüssig) geklammert:
(((42 * (hoch (2*3) ((fib 17)+4))) + 21) - (((hoch 47 11) * 3)) - (fib (((hoch (2+3)) (fib 21)) * 2)))
minimale Anzahl an Klammern ohne Bedeutungsänderung:
42 * hoch (2*3) (fib 17+4) + 21 - hoch 47 11 * 3 - fib (hoch (2+3) (fib 21) * 2)
Panikfeherbehandlung ist immer möglich, mit Auffangwerten aber nicht. Warum?
Panikfehlerbehandlung bedeutet, dass die Programmauswertung durch den Aufruf der vordefinierten error Funktion unwiderruflich abgebrochen wird. Da error echt polymorph ist (error :: String -> a) kann es im Rumpf jeder Funktion aufgerufen werden, daher immer möglich.
Ein Auffangwert retournieren bedeutet einen besonderen Wert zurückzugeben an dem erkennbar ist, dass ein Fehler aufgetreten ist. In gewissen Fällen lässt sich jedoch kein Wert angeben der Sinn ergibt, wie im Beispiel kopf ersichtlich:
kopf :: [a] -> a
kopf (u:_) = u
kopf [] = ???
Welches Resultat liefert die Folgende Zeile?
a = [(x,y,z) | x <- [1,2], y <- [3,4], z <- [5,6]]
Kann gelesen werden wie eine dreifach verschachtelte Schleife
for i in range (1,2):
for j in range (3,4):
for k in range (5,6):
print((i,j,k))
->> [(1,3,5),(1,3,6),(1,4,5),(1,4,6),(2,3,5),(2,3,6),(2,4,5),(2,4,6)]
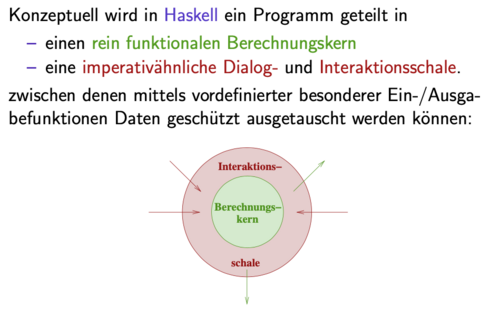
Warum stellen Ein- und Ausgabe eine Herausforderung für funktionale Programmiersprachen dar? Wie wurde dieses Problem in Haskell gelöst?
Funktionale Programmiersprachen sind gänzlich frei von Seiteneffekten und damit referentiell transparent. Input/Output Operationen sind aber inhärent seiteneffektbehaftet. Sie durchbrechen eigentlich die Eigenschaft referentieller Transparenz.
Die Lösung in Haskell besteht daraus, dass Werte von Input/Output Operationen durch unterschiedliche Typisierung (vom Typ IO) strikt von Werten reiner funktionaler Typen getrennt werden. Man kann sich vorstellen, dass es einen funktionalen Kern von Haskell gibt der von einer Input/Output Hülle umgeben ist. Aus dem Kern kann man in die Hülle, aber umgekehrt nur in sichergestellter Form, sodass referentielle Transparenz im Kern bestehen bleibt.
Was ist mit der Aussage gemeint, dass rein funktionale Programme zustandslos sind?
Aus einem rein funktionalen Programm heraus ist es nicht möglich, den Speicher anzusprechen und Speicherinhalte zu verändern. Speicher nicht veränderbar => Programm zustandslos.
Was ist eine verschleiernde Fehlerbehandlung?
Fehlerbehandlung mit Auffangwerten ohne explizite Nutzung der error Methode. Wenn der im Fehlerfall gelieferte Wert auch das Resultat einer regulär terminierenden Berechnung sein kann lässt sich unter Umständen nicht erkennen, ob ein Fehler aufgetreten ist oder nicht: der Fehler ist verschleiert.
Erklären Sie das Generator/Filter Prinzip anhand eines Beispiels
Beispiel: Berechnung der geraden natürlichen Zahlen. Mittels theNaturals als Generator wird der Strom an natürlichen Zahlen erzeugt. Mit filter werden die geraden Zahlen aus dem Strom herausgeholt.
theNaturals = [1..]
theEvenNaturals = [ n | n <- theNaturals, n `mod` 2 == 0 ]
Wichtige Funktionen[Bearbeiten | Quelltext bearbeiten]
Bitte erweitern um Funktionen die ihr für wichtig erachtet!
map[Bearbeiten | Quelltext bearbeiten]
map :: (a -> b) -> [a] -> [b]
Anwendung einer Funktion auf jedes Element einer Liste
Implementierung
-- rekursiv
map f [] = []
map f (l:ls) = (f l) : map f ls
-- listenkomprehension
map f ls = [f l | l <- ls]
Anwendungsbeispiele
map (+2) [1,2,3] ->> [3,4,5]
map square [2,4..10] ->> [4,16,36,64,100]
filter[Bearbeiten | Quelltext bearbeiten]
filter :: (a -> Bool) -> [a] -> [a]
Herausfiltern von Elementen die Bedingung einer Funktion nicht erfüllen
Implementierung
-- rekursion
filter p [] = []
filter p (l:ls)
| p l = l : filter p ls
| otherwise = filter p ls
-- listenkomprehension
filter p ls = [l | l <- ls, p l]