TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 191
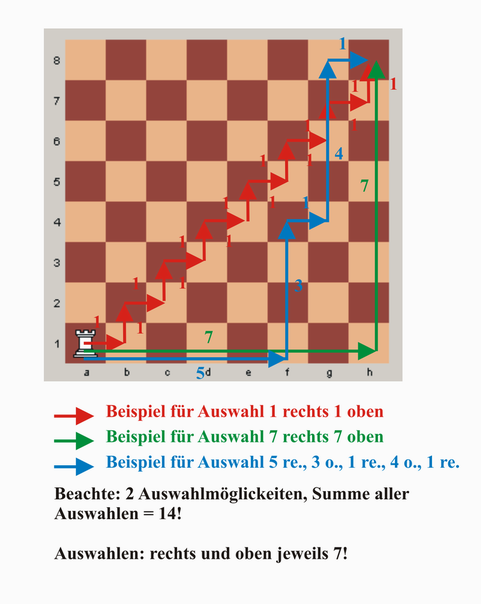
Ein Turm soll auf einem Schachbrett von der linken unteren Ecke in die rechte obere Ecke ziehen. Wieviel verschiedene Wege gibt es, wenn der Turm nie nach links oder nach unten ziehen darf, d.h. bei jedem Schritt nur ein oder mehrere Felder nach rechts oder nach oben?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Eine Grafik zur Veranschaulichung:
Wir stellen fest, dass
- der Turm immer zwei Möglichkeiten hat wohin er ziehen kann (rechts, oben)
- der Turm mindestens 1 Feld nach rechts ziehen kann und maximal 7 (analog nach oben)
- bedingt durch die Einschränkung des Schachbrettes können max. 7 Züge nach rechts und ebensoviele max. nach oben ausgeführt werden
- die Summe der o.g. Maxima ist 14
Man kann die möglichen Zugkombinationen als Permutation mit Wiederholung anschreiben.
Kombinationen.
Eine zweite Anschauung:
- ein Move des Turms besteht darin, dass er GENAU 1 Feld entweder nach rechts oder nach oben zieht.
- Damit der Turm vom linken unteren Eck zum rechten oberen kommt muss er GENAU 7x NACH RECHTS UND 7x NACH OBEN FAHREN, wobei es egal ist, in welcher Reihenfolge das geschieht.
zwei Möglichkeiten für eine gültige Sequenz an Turmzügen lauten (O=oben, R=rechts)
1) O O O O O O O R R R R R R R
2) O R O R O R O R O R O R O R (7x O und 7x R, die Gesamtzahl der Züge beträgt somit 14)
Die Anzahl an unterschiedlichen Möglichkeiten durch Vertauschung von O's und R's würde 14! betragen, wenn die O's und R's unter sich UNTERSCHEIDBAR wären. Das sind sie aber nicht, deshalb muss die Anzahl der Möglichkeiten einmal wegen R durch 7! und einmal wegen O durch 7! dividiert werden. Soviele Möglichkeiten fallen nämlich auf EINE beliebige Zugsequenz, wenn sie unterscheidbar wären.
Lösung von newtron alex[Bearbeiten | Quelltext bearbeiten]
Eine weitere Interpretation ist: man betrachte die Möglichkeiten, ein Feld über seine benachbarten Felder zu erreichen. Am Besten startet man von links unten und arbeitet sich nach rechts oben durch. z.B. das Feld 1,0 (Achtung: Das ist die zweite Zeile, 1. Spalte von unten links!) erreicht man über 1 möglichen Weg von 0,0, das Feld 1,1 über 2 mögliche Wege, das Feld 1,2 über drei mögliche usw. Wenn man zu einem Feld weiter rechts oben gelangt, stellt sich heraus, dass die Anzahl der Möglichkeiten dorthin zu gelangen gleich der Summe der Möglichkeiten vom linken benachbarten Feld plus dem unteren benachbarten Feld sein muss. Man kann ja nur von diesen beiden Richtungen kommen und die Anzahl der möglichen Wege addiert sich einfach. Somit bildet sich ein Gebilde, das dem Pascal'schen Dreieck entspricht. Jetzt muss man sich nur noch überlegen, wie man auf n und k kommt. n stellt die Zeile im Pascalschen Dreieck dar, was in unserem Fall den Diagonalen des Schachbretts entspricht. Um nun mit der Diagonale vom Punkt 0,0 zum Punkt 7,7 (Ziel im 8x8-Schachbrett) zu gelangen, muss man 7 Schritte nach oben machen (n beginnt bei 0) und von dort 7 Schritte nach rechts. Somit liegt der Punkt 7,7 (das 64te Feld => Ziel) auf der 14. Diagonale => n = 14. Analog dazu verhält es sich mit der Spalte (=k) im Pascalschen Dreieck, diese lautet 7 (wir befinden uns am Schachbrett ja im 8ten Feld von links, von 0 gezählt Spalte 7). Die Lösung ergibt sich aus dem Binomialkoeffizienten (n über k), der ja die Koeffizienten des pascalschen Dreieck liefert. Siehe Lösung von mnemetz.
Habe leider keine Zeit, das graphisch aufzubereiten, aber wenn man versucht, die Möglichkeiten, ein Feld zu erreichen, sukzessive von links unten beginnend auszufüllen und aufzuaddieren, sollte alles glasklar werden.