TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 289
Man bestimme die starken Zusammenhangskomponenten und die Reduktion des Graphen .
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theoretische Grundlagen (von Baccus)[Bearbeiten | Quelltext bearbeiten]
- Ein ungerichteter Graph G heißt zusammenhängend, wenn jeder Knoten von jedem Knoten aus erreichbar ist: Kantenfolge, die und verbindet.
- In einem gerichteten Graphen
- heißen jene Knoten stark zusammenhängend, die mit anderen Knoten in beiden Richtungen verknüpft sind: .
- Knoten heißen schwach zusammenhängend, wenn sie im Schatten des Urgraphen gegenseitig erreichbar sind.
Ein gerichteter Graph zerfällt daher u.U. in mehrere Zusammenhangskomponenten, die in sich stark zusammenhängend sind, aber nicht untereinander.
Bei der Reduktion eines Graphen werden die starken Zusammenhangskomponenten zu einem Punkt (Knotensammlung) zusammengefaßt.
Stark zusammenhängend[Bearbeiten | Quelltext bearbeiten]
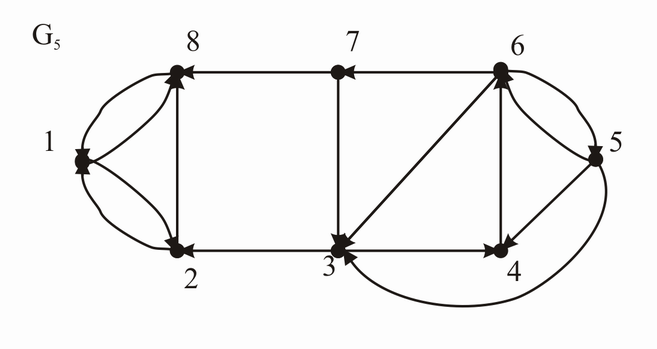
sind daher (nach Anschauung) die Knoten (1,2,8) und (3,4,5,6,7).
Reduziert[Bearbeiten | Quelltext bearbeiten]
sieht der Graph also so aus:
.
Theoretische Grundlagen (von Jazzlyn)[Bearbeiten | Quelltext bearbeiten]
- Wir haben einen gerichteten Graphen . Zwei Ecken (Knoten) und sind stark zusammenhängend, wenn sie direkt und in beide Richtungen miteinander verbunden sind.
- Die Menge aller Ecken (Knoten), die zu und einen Weg haben und von und erreichbar sind, sind die starken Zusammenhangskomponenten.
Lösung[Bearbeiten | Quelltext bearbeiten]
Seit WS 2016 ist die Aufgabenstellung wohl überarbeitet worden. die Reduktion ist nicht mehr gefragt!
Bei dieser Fragestellung werden die starken Zusammenhangskomponenten gesucht. Wir gehen daher in zwei Schritten vor. Zuerst bestimmen wir die Knoten, die stark zusammenhängend sind.
Für die linke Seite wären das: {1, 2, 8} Für die rechte Seite: {6, 5}
Damit sind wir aber noch nicht fertig, denn wir suchen die starken Zusammenhangskomponenten.
Für die linke Seite bleibt es bei {1, 2, 8}, da die Pfeile von 8 und 2 nicht nach rechts gehen. Auf der rechten Seite ergibt sich {6, 5, 3, 4, 7}. 3, 4 und 7 kommen somit dazu.
[Theoretische Grundlagen (von mnemetz) [unklar]][Bearbeiten | Quelltext bearbeiten]
Ein ungerichteter Graph G heißt zusammenhängend, wenn jeder Knoten y von jedem Knoten x aus erreichbar ist.
In einem gerichteten Graph fasst man jene Knoten zu einer starken Zusammenhangskomponente zusammen, die selbst von jedem dieser Knoten erreichbar sind. Sollte ein Knoten nur in einer Richtung erreichbar sein, so wird er selbst zu einer starken Zusammenhangskomponente.
Bei der Reduktion eines Graphen werden die starken Zusammenhangskomponenten zu einem Punkt zusammengefasst und dann verbunden.
[Lösungsvorschlag von menemetz (inkorrekt)][Bearbeiten | Quelltext bearbeiten]
Starke Zusammenhangskomponenten[Bearbeiten | Quelltext bearbeiten]
Starke Zusammenhangskomponenten sind:
- (Einser-Zyklus)
- 1-8
- 1-2
- 1-2-8
- (Vierer-Zyklus)
- 4-6-7-3
- 4-6-3
- (Fünfer-Zyklus)
- 5-4-6
- 5-3-4-6
Graphentheoretische Reduktion[Bearbeiten | Quelltext bearbeiten]
1 2 8 5 3 4 6 *--------->*<-----------* 4 6 7 3