TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 325

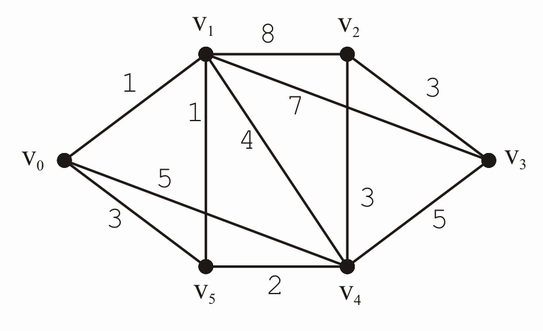
Im nachstehenden bewerteten Graphen bestimme man den Entfernungsbaum bezüglich des Knotens $v_{0}$.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag von mnemetz

Entfernungsbaum

Entfernungsbäume werden in gewichteten Graphen erstellt, wenn von einem Startpunkt aus in mehreren Zwischenschritten klar sein soll, wie viel der Weg zu diesem und jenen Punkt insgesamt "kostet".

Um einen Entfernungsbaum zu erstellen geht man wie folgt vor:

1. Die Wurzel ist die Ecke s (Startpunkt)
2. Ecken des Baumes sind die von s aus erreichbaren Ecken des Graphen
3. Als Kanten werden die kürzesten Wege von der Ecke s zur entsprechenden Ecke eingezeichnet. Schon vorhandene kürzeste Wege werden benutzt
4. Die Kanten werden mit den Abständen zwischen ihren Ecken bewertet.

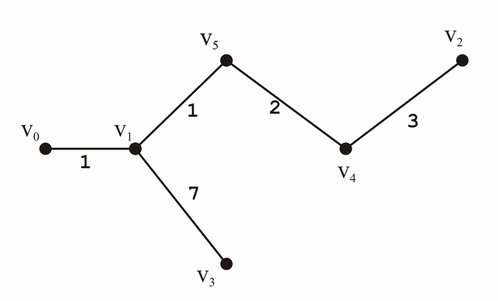
Man kann aus einem Entfernungsbaum die Abstände zur Ecke s sofort ablesen. Dazu geht man einfach ”den Baum nach unten” bis zur interessierenden Ecke und addiert die Bewertungen. Allerdings sind Entfernungsbäume nicht eindeutig (weil es mehrere kürzeste Wege geben kann).

Anders hätte man fragen können: Gesucht sei der minimal spannende Baum!

[Anmerkung von David Mihola: Das mit dem minimal spannenden Baum stimmt nicht. Der minimale spannende Baum muss nicht dieselben Kanten beinhalten wie ein Entfernungsbaum. In diesem konkreten Fall müsste der minimal spannende Baum statt der Kante v1-v3 die Kante v2-v3 enthalten, da 3 weniger ist als 7. (Vgl. Kruskal-Algorithmus)]

Entfernungsbaum mit Tabelle erstellen

Weg $v_{0}\rightarrow v_{3}$ - kürzester Weg zwischen diesen Punkten mit dem Dikstra-Algorithmus herausfinden!

Anmerkung Iteration	$v_{0}$	$v_{1}$	$v_{2}$	$v_{5}$	$v_{4}$	$v_{3}$	Auswahl	Vorgänger
1		1	$\infty$	3	$\infty$	$\infty$	$v_{1}$	$v_{0}$
2			9	2	5	8	$v_{3}$	$v_{1}$

Halten wir nun den kürzesten Weg von $v_{0}$ nach $v_{3}$ mit $\mathbf {v_{0}\rightarrow v_{1}\rightarrow v_{3}}$ fest!

Anmerkung: Das Ergebnis stimmt zwar, aber ich denke das der Algorythmus zu früh "abgebrochen" wurde. BTW fehlt bei der 1ten Iteration die Verbindung von $v_{0}\rightarrow v_{4}$ mit dem Gewicht 5

Weg $v_{0}\rightarrow v_{1}$ - kürzester Weg zwischen diesen Punkten mit dem Dikstra-Algorithmus herausfinden!

Anmerkung Iteration	$v_{0}$	$v_{1}$	$v_{2}$	$v_{5}$	$v_{4}$	$v_{3}$	Auswahl	Vorgänger
1		1	3	$\infty$	$\infty$	$\infty$	$v_{1}$	$v_{0}$

Halten wir nun den kürzesten Weg von $v_{0}$ nach $v_{1}$ mit $\mathbf {v_{0}\rightarrow v_{1}}$ fest! (führt schon entlang eines Weges nach $v_{3}$!).

Weg $v_{0}\rightarrow v_{2}$ - kürzester Weg zwischen diesen Punkten mit dem Dikstra-Algorithmus herausfinden!

Anmerkung Iteration	$v_{0}$	$v_{1}$	$v_{2}$	$v_{5}$	$v_{4}$	$v_{3}$	Auswahl	Vorgänger
1		1	3	$\infty$	$\infty$	$\infty$	$v_{1}$	$v_{0}$
2			9	2	5	8	$v_{5}$	$v_{1}$
3					4		$v_{4}$	$v_{5}$
4			7				$v_{2}$	$v_{4}$
5			9	2	5	8	$v_{4}$	$v_{1}$
6			8				$v_{2}$	$v_{4}$
7			9				$v_{2}$	$v_{1}$

Halten wir nun den kürzesten Weg von $v_{0}$ nach $v_{2}$ mit $\mathbf {v_{0}\rightarrow v_{1}\rightarrow v_{4}}$ fest!

Weg $v_{0}\rightarrow v_{5}$ - kürzester Weg zwischen diesen Punkten mit dem Dikstra-Algorithmus herausfinden!

Anmerkung Iteration	$v_{0}$	$v_{1}$	$v_{2}$	$v_{5}$	$v_{4}$	$v_{3}$	Auswahl	Vorgänger
1		1	3	$\infty$	$\infty$	$\infty$	$v_{1}$	$v_{0}$
2				2			$v_{5}$	$v_{1}$

Halten wir nun den kürzesten Weg von $v_{0}$ nach $v_{5}$ mit $\mathbf {v_{0}\rightarrow v_{1}\rightarrow v_{5}}$ fest!

Weg $v_{0}\rightarrow v_{4}$ - kürzester Weg zwischen diesen Punkten mit dem Dikstra-Algorithmus herausfinden!

Anmerkung Iteration	$v_{0}$	$v_{1}$	$v_{2}$	$v_{5}$	$v_{4}$	$v_{3}$	Auswahl	Vorgänger
1		1	3	$\infty$	$\infty$	$\infty$	$v_{1}$	$v_{0}$
2					5		$v_{4}$	$v_{1}$
3				2			$v_{5}$	$v_{1}$
4					4		$v_{4}$	$v_{5}$

Halten wir nun den kürzesten Weg von $v_{0}$ nach $v_{4}$ mit $\mathbf {v_{0}\rightarrow v_{1}\rightarrow v_{5}\rightarrow v_{4}}$ fest!

[Anmerkung von David Mihola: Ich weiß nicht genau, was hier passiert: Es müsste doch reichen, ein einziges Mal den Dijkstra-Algorithmus durchzuführen und zwar so lange, bis jeder Knoten einmal der Knoten mit der geringsten Total-Entfernung zum Startknoten war - dann hat man nämlich für jeden Knoten den minimalen Abstand zum Startknoten gefunden.]

[Anmerkung 2: Dieses YouTube Video erklärt die einzelnen Schritte des Dijkstra Alogrithmus sehr gut mit einem sehr ähnlichen Beispiel: https://www.youtube.com/watch?v=bZkzH5x0SKU]

Gesamte Tabelle

vo	v1	v2	v3	v4	v5	Auswahl	Vorgänger
0	-	-	-	-	-	v0	-
	1	-	-	5	3	v1	v0
		9	8	5	2	v5	v1
		9	8	4		v4	v5
		7	8			v2	v4
			8			v3	v1

Zur Überprüfung

# LG Markus K.
import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd

def dijkstra(graph: dict, start: str, end: str) -> pd.DataFrame:
    # init stuff
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    unvisited_vertices = set(graph)
    steps_data = []
    step = 1
    prev_vertex = {vertex: None for vertex in graph}

    while unvisited_vertices:
        current_vertex = min(unvisited_vertices, key=lambda vertex: distances[vertex])
        unvisited_vertices.remove(current_vertex)

        step_data = {'Step': step, 'Visiting': current_vertex, 'Previous': prev_vertex[current_vertex]}
        for vertex, distance in distances.items():
            step_data[vertex] = distance
        steps_data.append(step_data)

        for neighbor, weight in graph[current_vertex].items():
            potential_distance = distances[current_vertex] + weight
            if potential_distance < distances[neighbor]:
                distances[neighbor] = potential_distance
                prev_vertex[neighbor] = current_vertex

        step += 1

    path = []
    current = end
    while current is not None:
        path.insert(0, current)
        current = prev_vertex[current]

    path_df = pd.DataFrame(path, columns=['Shortest Path'])

    return pd.DataFrame(steps_data), path_df

weighted_graph = {
    'v_0': {'v_1': 1, 'v_5': 3, 'v_4': 5},
    'v_1': {'v_0': 1, 'v_5': 1, 'v_2': 8, 'v_4': 4, 'v_3': 7},
    'v_2': {'v_1': 8, 'v_3': 3, 'v_4': 3},
    'v_3': {'v_1': 7, 'v_2': 3, 'v_4': 5},
    'v_4': {'v_0': 5, 'v_1': 4, 'v_2': 3, 'v_3': 5, 'v_5': 2},
    'v_5': {'v_0': 3, 'v_1': 1, 'v_4': 2},
}

# ---------------- visualize graph --------------------------
G = nx.Graph(weighted_graph)
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_size=700, node_color='skyblue', 
        font_size=10, font_color='black', font_family='calibri')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.show()

start_vertex = 'v_0'
end_vertex = 'v_3'
steps_df, path_df = dijkstra(weighted_graph, start_vertex, end_vertex)

print("Steps:")
display(steps_df)

print("\nShortest Path:")
display(path_df)

Webressourcen

• Entfernungsbäume - der Algorithmus von Dijkstra
• Informatik-Forum Thread 1
• http://www.math2.rwth-aachen.de/~uebung/GT/vorl_gt.pdf - Seite 25, Def. Entfernungsbaum
• http://www.msl.uni-bonn.de/vorlesung/vermessung/skripte/md-9899.pdf - Seite 14
• http://www.fs-mathematik.uni-kiel.de/fileadmin/download/inf2/Skript.pdf - Seite 104