TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 157
Sei monoton fallend und differenzierbar. Man zeige, dass dann für alle gilt.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösung[Bearbeiten | Quelltext bearbeiten]
Wir machen hier einen indirekten Beweis. Wir nehmen an, dass es ein gibt für welches gilt und zeigen, dass dann nicht monoton fallend ist.
Wenn ist, muss es, da die Ableitung von f stetig ist, eine ganze Umgebung von geben, für welche ist.
Sei a und b aus dieser Umgebung und a < b. Dann folgt aus dem Mittelwertsatz der Differentialrechnung, dass es ein c gibt für das gilt:
Da ist(c liegt ja zwischen a und b und somit in der Umgebung um in der ist) und a < b folgt:
Damit f aber monoton fallend ist müsste für alle a, b mit a < b gelten, dass
f ist daher nicht monoton fallend und wir sind fertig.
Alternative Lösung[Bearbeiten | Quelltext bearbeiten]
Nachdem Beispiel 14 und 15 zusammen gehören hier eine alternative (einfachere) Begründung:
Beispiel 14[Bearbeiten | Quelltext bearbeiten]
Nachdem die Funktion monoton fallend und differenzierbar ist muss folgendes gelten
mit
Für den 1.Fall, dass gilt also:
Für den 2.Fall, dass gilt also:
Beispiel 15[Bearbeiten | Quelltext bearbeiten]
Analog wie Beispiel 14:
Nachdem die Funktion streng monoton fallend und differenzierbar ist muss folgendes gelten
mit
Für den 1.Fall, dass gilt also:
Für den 2.Fall, dass gilt also:
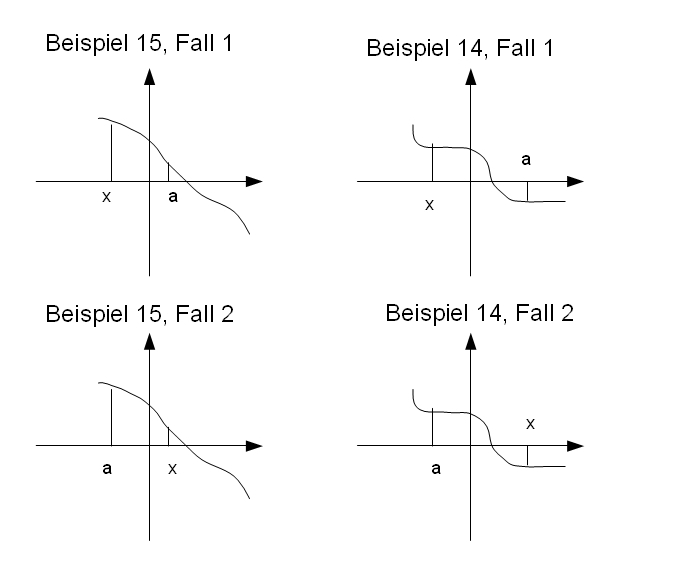
Skizze[Bearbeiten | Quelltext bearbeiten]
--W1n5t0n 15:24, 31. Jan. 2010 (CET)
Quelle[Bearbeiten | Quelltext bearbeiten]
Panholzer Beispielsammlung WS05 / SS06 Beispiel 437 / SS07 Beispiel 13