TU Wien:Mathematik 1 VO (Karigl)/Prüfung 2010-07-01

Angabe

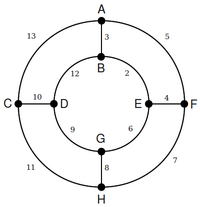
Angabe der Prüfung aus Mathematik 1 für Informatik (Karigl) am 1.7.2010

Beispiel 1: Minimaler Spannbaum

Verbindung mehrerer Universitäten über ein high-speed fibre Datennetz. Berechne die Kosten für ein minimales Datennetz.

Beispiel 2: Lineares Gleichungssystem

Überprüfe folgendes Gleichungssystem auf Lösbarkeit und gib, sofern sie existieren, alle Lösungen an.

${\begin{matrix}x_{1}&+&2x_{2}&-&3x_{3}&=&-4\\4x_{1}&-&15x_{2}&+&11x_{3}&=&7\\-x_{1}&+&x_{2}&&&=&1\end{matrix}}$

Beispiel 3: Taylorreihen

Leite für alle unendichen Reihen für $sin(x)$ und $cos(x)$ durch Entwickeln in $f(x)$ eine Taylorreihe mit Entwicklungspunkt $x_{0}=0$ her, und zeige damit, dass $e^{ix}=cos(x)+i\cdot sin(x)$    $x\in \mathbb {R}$

Beispiel 4: EAN-Code (ISBN)

Der EAN-13 (European Article Number) Code ist wiefolgt aufgebaut: $a_{1}+3a_{2}+a_{3}+...+3a_{12}+p\equiv 0\,mod\,10$

a) Berechne die Prüfziffer p für den EAN 400781750216p

b) Beweise, dass der EAN-Code Einzelfehler immer erkennt.

Beispiel 5: Funktionen, Ableitung, Stetigkeit

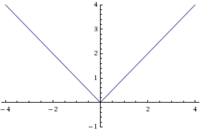
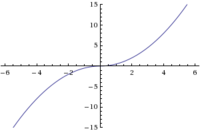
Skizziere die Folgenden Funktiongraphen

$f(x)=|x|\,$

$g(x)={\frac {1}{2}}x\cdot |x|$

• ist f(x) stetig auf $\mathbb {R}$
• ist f(x) differenzierbar auf $\mathbb {R}$?
• für f(x) gilt?
  • f'(x) = 1 für x > 0
  • f'(x) = -1 für x < 0
  • f'(x) = 0 für x = 0
• gilt g'(x) = f(x) für alle x aus?
• ist jede im Punkt $x_{0}$ stetige Funktion differenzierbar?

Lösung

Lösungsvorschlag Bsp 1 von Green Mamba

Sortieren der Kanten nach Gewicht (Algorithmus von Kruskal)

• BE=2
• AB=3
• EF=4
• AF=5 bildet Kreis
• EG=6
• FH=7
• GH=8 bildet Kreis
• DG=9
• CD=10
• CH=11 bildet Kreis
• BD=12 bildet Kreis
• AC=13 bildet Kreis

diejenigen Kanten, die keinen Kreis bilden bilden die Lösungsmenge

-> Kantensumme=2+3+4+6+7+9+10 = 41

Lösungsvorschlag Bsp 2 von Thomas

Das Gleichungsystem in erweiterter Koeffizientenmatrix-Form aufschreiben und mit elementaren Zeilenumformungen anfangen Nullen zu erzeugen:

$(A{\boldsymbol {b}})={\begin{pmatrix}1&2&-3&-4\\4&-15&11&7\\-1&1&0&1\end{pmatrix}}$	$a_{2}'=-4\cdot a_{1}+a_{2}$ $a_{3}'=1\cdot a_{1}+a_{3}$
$(A{\boldsymbol {b}})'={\begin{pmatrix}1&2&-3&-4\\0&-23&23&23\\0&3&-3&-3\end{pmatrix}}$	$a_{2}''={\frac {1}{23}}\cdot a_{2}'$
$(A{\boldsymbol {b}})''={\begin{pmatrix}1&2&-3&-4\\0&-1&1&1\\0&3&-3&-3\end{pmatrix}}$	$a_{3}'''=3\cdot a_{2}''+a_{3}''$
$(A{\boldsymbol {b}})'''={\begin{pmatrix}1&2&-3&-4\\0&-1&1&1\\0&0&0&0\end{pmatrix}}$	$a_{1}''''=2\cdot a_{2}'''+a_{1}'''$ $a_{2}''''=a_{2}'''\cdot -1$
$(A{\boldsymbol {b}})''''={\begin{pmatrix}1&0&-1&-2\\0&1&-1&-1\\0&0&0&0\end{pmatrix}}$

Aus der halbdiagonalen Form entnehmen wir, dass das Gleichungssystem eine mehrdeutige Lösung besitzt.

${\begin{matrix}x_{1}&&&-&x_{3}&=&-2\\&&x_{2}&-&x_{3}&=&-1\end{matrix}}$

wir setzen $x_{3}=t$ und formen um

${\begin{matrix}{\boldsymbol {x}}_{1}&=&t-2\\{\boldsymbol {x}}_{2}&=&t-1\end{matrix}}$

$t$ ist also frei wählbar (lässt sich leicht mit Einsetzen überprüfen).

Lösungsvorschlag Bsp 3 von Juggl3r

Die Taylorreihe ist gegeben durch folgende Formel:

f(x) = f(x0) + f(1)(x0)*x + (f(2)(x0)*x^2) / 2! + (f(3)(x0)*x^3) / 3! + ...

D.h. wir benötigen zuerst einmal die Ableitungen von sin und cos.

f(x) = sin(x)

f(1)(x) = cos(x)

f(2)(x) = -sin(x)

f(3)(x) = -cos(x)

f(4)(x) = sin(x)

f(5)(x) = cos(x)

....

f(x) = cos(x)

f(1)(x) = -sin(x)

f(2)(x) = -cos(x)

f(3)(x) = sin(x)

f(4)(x) = cos(x)

f(5)(x) = -sin(x)

....

So und nun setzen wir ein:

sin(x) = sin(0) + cos(0)*x - sin(0)*x^2/2! - cos(0)*x^3/3! + sin(0)*x^4/4! + cos(0)*x^5/5! --++ ...

sin(x) = x - x^3/3! + x^5/5! - x^7/7! +- ...

=> Das ist die Reihendarstellung von Sinus

Das gleiche für cos:

cos(x) = cos(0) - sin(0)*x - cos(0)*x^2/2! + sin(0)*x^3/3! + cos(0)*x^4/4! --++...

cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + x^8/8! -+...

Nun müssen wir noch zeigen, dass cos(x) + i*sin(x) = e^(i*x) ist.

Dazu entwickeln wir e^(i*x) auch in einer Taylorreihe, also leiten wir es zuerst einmal ab:

f(x) = e^(ix)

f(1)(x) = e^(ix)*i

f(2)(x) = e^(ix)*i^2 = - e^(ix)

f(3)(x) = e^(ix) * -i

f(4)(x) = e^(ix)

f(5)(x) = e^(ix)*i

...

e^(ix) = e^0 + e^0*i*x - e^0*x^2/2! -e^0*i*x^3/3! + e^0*x^4/4! + e^0*i*x^5/5! --++...

e^(ix) = 1 + i*x - x^2/2! - i*x^3/3! + x^4/4! + i*x^5/5! --++...

Wenn wir nun: i*sin(x) + cos(x) berechnen, erhalten wir:

i*sin(x) = i*(x - x^3/3! + x^5/5! - x^7/7! +- ...)

+

cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + x^8/8! -+...

=

cos(x) + i*sin(x) = 1 + i*x - x^2/2! - i*x^3/3! ++--

(Ich habe in einer unendlichen Summe nun Summanden vertauscht. Dies ist eigentlich nicht zulässig, aber Herr Karigl hat in der Vorlesung gesagt, dass dies hier funktioniert.) Wie zu sehen ist, ist dies die selbe Darstellung wie e^(ix), also ist cos(x) + i*sin(x) = e^(ix), was zu beweisen war. qed

Lösungsvorschlag Bsp 4 von Thomas

a)

Die Prüfziffer des EAN-13 ist die Differenz der Summe zum nächsten Vielfachen von 10.

400781750216p

4 + 3*0 + 0 + 3*3 + ... = 83

90 ist das nächste Vielfache von 10

90 - 83 = 7, p = 7

b)

Annahme:

2 Korrekte EAN Codes

Beide EAN Codes unterscheiden sich an Stelle n

.....a.......

.....b.......

Fall 1:

n'tes Bit ist das Prüfbit.

Trivialer Fall, da alle anderen Bits sonst gleich sind und keine 2 unterschiedlichen Prüfbits rauskommen können.

Fall 2:

n'tes Bit ist nicht das Prüfbit.

Die Formel für EAN Code lautet: a1 + 3a2 + a3 + 3a4 +...+a11+3a12 + p kongruent 0 mod 10

Nun formen wir auf p um ergibt: p kongruent -a1 -3a2 -a3 -...- 3a12 mod10

Da aber -1 kongruent 9 mod 10 ist (einfach -1+10 rechnen) und -3 kongruent 7 mod 10 folgt:

p kongruent 9a1 + 7a2 + 9a3 +...+ 7a12 mod10.

Da wir nun wissen, dass die Prüfbits beider EAN Codes gleich sind, können wir diese Formel gleich setzen.

Weiters sind alle Summen bis auf Stelle n gleich, weshalb wir für die restlichen Summen S schreiben können:

S + x*a kongruent S + x*b mod 10

wobei x e {7,9} (da dies die Koeffizienten sind und wir nicht wissen, ob n gerade oder ungerade ist)

weiters ist a,b e {0,1,2,..,8,9}

Nun subtrahieren wir S und x*b. Weiters heben wir anschließend x heraus:

x(a-b) kongruent 0 mod 10

Da ggT(x,10) = 1 ist (da x nur 7 und 9 sein kann), dürfen wir kürzen.

=> a-b kungruent 0 mod 10

=> a kongruent b mod 10

Da nun aber a,b e {0,...,9} sind, aber beide den gleichen Rest haben müssen bei einer Division von 10, muss a = b gelten. Das ist wieder ein Widerspruch zu unserer Annahme, weshalb 2 EAN Codes, welche korrekt sind, sich nicht unterscheiden können. q.e.d.

Lösungsvorschlag Bsp 5 von Thomas

Fehler dürfen gerne behoben werden ;-)

$f(x)=|x|\,$	$g(x)={\frac {1}{2}}x\cdot |x|$

• ist f(x) stetig auf $\mathbb {R}$?
  • ja (leicht zu sehen)
• ist f(x) differenzierbar auf $\mathbb {R}$?
  • nein f(x) ist im punkt x=0 nicht differenzierbar (siehe wikipedia eintrag zur betragsfunktion)
• für f(x) gilt?
  • f'(x) = 1 für x > 0
    • ja
  • f'(x) = -1 für x < 0
    • ja
  • f'(x) = 0 für x = 0
    • nein (siehe frage 2)
• gilt g'(x) = f(x) für alle x aus ℝ?
  • hier bin ich mir nicht sicher. die ableitung von $x\cdot |x|$ ist auf jedenfall $2|x|$ (siehe buch s. 190 abb. 5.3), sinn würde es also machen.
    • Bei meiner Prüfungseinsicht sagte Prof. Karigl, dass die richtige Antwort Ja ist. --RavuAlHemio
• ist jede im Punkt $x_{0}$ stetige Funktion differenzierbar?
  • nein jede differenzierbare funktion ist stetig, die umkehrung gilt aber nicht