TU Wien:Mathematik 2 UE (diverse)/Übungen SS07/Beispiel 97

Man ermittle die Gleichungen der Tangenten aus dem Punkt $(-1,1)$ an die Hyperbel $xy=1$.

Lösungsvorschlag von Baccus

Ansatz der Tangentengleichung

Geradengleichung durch den Punkt $(-1,1)$:

Geradengleichung in "Einpunktform" durch Fixpunkt $(x_{f},y_{f})$:

$y-y_{f}=k\cdot (x-x_{f})$

Eine Gerade durch (-1, 1) wird also durch die Gleichung $y=1+k\cdot (x-(-1))$ beschrieben. Dadurch ist der erste Fixpunkt der Tangente festgelegt.

Steigung der Tangente

Die Tangentensteigung im Berührungspunkt $(x_{b},y_{b})$ der Hypräbel entspricht der ersten Ableitung der Hyperbel-Gleichung an $x_{b}$, und ist natürlich auch gleich der Steigung $k$ in der Tangentengleichung.

Die Einheits-Hyperbel ist gegeben durch $xy=1$, d.h. $y=1/x\Longrightarrow$

$k=\left(1/x_{b}\right)'=\left(x_{b}^{-1}\right)'=-1\cdot x_{b}^{-2}=-{\tfrac {1}{x_{b}^{2}}}$.

Festlegung des Berührungspunktes

Graphische Auswertung

Im Berührungspunkt müssen die Koordinaten des Punktes auf der Hyperbel mit denen des Punktes auf der Tangenten-Gerade zusammenfallen; d.h. sowohl die Tangentengleichung, wie auch die Hyperbel-Gleichung muß für $x_{b}$ denselben y-Wert liefern:

$y_{b_{Gerade}}=1+(x_{b}+1)\cdot k\quad =\quad 1/x_{b}=y_{b_{Hyperbel}}$

Auflösung der Gleichung:

${\begin{aligned}y_{b}=\;1+(x_{b}+1)\cdot {\frac {-1}{x_{b}^{2}}}&=1/x_{b}\\1-{\frac {x_{b}+1}{x_{b}^{2}}}&=1/x_{b}\\1&={\tfrac {1}{x_{b}}}+{\tfrac {x_{b}+1}{x_{b}^{2}}}\\1&={\tfrac {1}{x_{b}}}+{\tfrac {x_{b}}{x_{b}^{2}}}+{\tfrac {1}{x_{b}^{2}}}\\1&={\tfrac {2}{x_{b}}}+{\tfrac {1}{x_{b}^{2}}}\qquad \vert \leftrightarrow \\-1+{\tfrac {2}{x_{b}}}+{\tfrac {1}{x_{b}^{2}}}&=0\qquad \vert \cdot x_{b}^{2}\\-x_{b}^{2}+2x_{b}+1&=0\end{aligned}}$

Große Lösungsformel

Große Lösungsformel

$ax^{2}+bx+c=0\quad \Longrightarrow \quad x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$.

$\Rightarrow x_{b_{1,2}}={\frac {-2\pm {\sqrt {2^{2}+4}}}{-2}}=1\mp {\sqrt {2}}$

Ergebnis

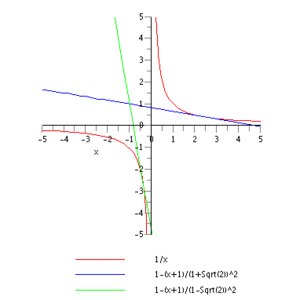
Durch Einsetzen der gefundenen Werte für $x_{b}$ in die Tangentengleichung erhält man: $y_{Tangente_{1,2}}=1-{\frac {x+1}{(1\mp {\sqrt {2}})^{2}}}$ (siehe Graphik).

--Baccus 01:33, 28. Apr 2007 (CEST)

Links

• Diskussion im Informatikforum
• Konversatorium: TU Wien:Mathematik 2 UE (diverse)/Konversatorium SS07 (vermischt mit SS08)/Tangenten