TU Wien:Mathematik 2 UE (diverse)/Übungen SS10/Beispiel 202

B sei das durch die Punkte (0, 0), (1, 1), (1,−2) und (4, 3) festgelegte konvexe Viereck. Berechnen Sie $\iint _{B}xy-x^{2}+y^{2}dxdy$

Vorschlag von crispy

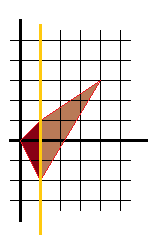
Man Teile den Bereich an der Geraden x = 1 in 2 Teile.

Das Integral über die X-Achse ist einfach - der Bereich geht von 0 bis 4 (bzw. von 0 bis 1 und 1 bis 4

Für die Y-Achse müssen wir Funktionen finden, die jedem x-Wert die passenden Grenzen zuordnen:

${\begin{aligned}\psi (x)&=x\\\varphi (x)&=-2x\\\psi '(x)&={\frac {2}{3}}x+{\frac {1}{3}}\\\varphi '(x)&={\frac {5}{3}}x-{\frac {11}{3}}\end{aligned}}$

Unsere Geraden sind gegeben durch 2 Punkte: $\psi ':(1,1),(4,3);\varphi :(1,-2),(4,3)$. die Steigung k der Gerade erhält man, indem man die Differenz in Y-Richtung durch die Differenz in X-Richtung dividiert: $k={\frac {x_{1}-x_{0}}{y_{1}-y_{0}}};\psi ':k={\frac {3-1}{4-1}}={\frac {2}{3}};\varphi :k={\frac {3-(-2)}{4-1}}={\frac {5}{3}}$.

Danach einfach einen gegebenen Punkt in die allgemeine Geradengleichung y = kx+d einsetzen, um d zu erhalten: $\psi ,(1,1):1={\frac {2}{3}}*1+d\Rightarrow d={\frac {1}{3}};\varphi ,(4,3):3={\frac {5}{3}}*4+d\Rightarrow d={\frac {-11}{3}}$

Unser Integral sieht dann so aus:

$\int _{0}^{1}\int _{\varphi (x)}^{\psi (x)}xy-x^{2}+y^{2}\,dy\,dx+\int _{1}^{4}\int _{\varphi '(x)}^{\psi '(x)}xy-x^{2}+y^{2}\,dy\,dx=?$

Dann mal los (ein Teil nach dem anderen, von innen nach außen)

$\int _{0}^{1}\int _{\varphi (x)}^{\psi (x)}xy-x^{2}+y^{2}\,dy\,dx=$	(nach y integrieren, x ist hier konstant)
$\int _{0}^{1}{\frac {xy^{2}}{2}}-x^{2}y+{\frac {y^{3}}{3}}|_{\varphi (x)}^{\psi (x)}\,dx=$	(Grenzen einsetzen)
$\int _{0}^{1}{\frac {xy^{2}}{2}}-x^{2}y+{\frac {y^{3}}{3}}|_{-2x}^{x}\,dx=$	(auswerten...)
$\int _{0}^{1}{\frac {x^{3}}{2}}-x^{3}+{\frac {x^{3}}{3}}-({\frac {x(-2x)^{2}}{2}}-x^{2}(-2x)+{\frac {(-2x)^{3}}{3}})\,dx=$	(ausmultiplizieren)
$\int _{0}^{1}-{\frac {x^{3}}{6}}-2x^{3}-2x^{3}+{\frac {8x^{3}}{3}})\,dx=$	(vereinfachen)
$\int _{0}^{1}{\frac {-x^{3}-12x^{3}-12x^{3}+16x^{3}}{6}}\,dx=$	(vereinfachen)
$\int _{0}^{1}-{\frac {3}{2}}x^{3}\,dx=$	(konstante herausziehen, integrieren)
$-{\frac {3}{2}}*{\frac {x^{4}}{4}}|_{0}^{1}=$
$-{\frac {3}{2}}*{\frac {1}{4}}={\underline {-{\frac {3}{8}}}}$

Der zweite Teil verläuft analog:

$\int _{1}^{4}\int _{\varphi '(x)}^{\psi '(x)}xy-x^{2}+y^{2}\,dy\,dx=$	(nach y integrieren, x ist hier konstant)
$\int _{1}^{4}{\frac {xy^{2}}{2}}-x^{2}y+{\frac {y^{3}}{3}}|_{\varphi '(x)}^{\psi '(x)}\,dx=$	(Grenzen einsetzen)
$\int _{1}^{4}{\frac {xy^{2}}{2}}-x^{2}y+{\frac {y^{3}}{3}}|_{{\frac {5}{3}}x-{\frac {11}{3}}}^{{\frac {2}{3}}x+{\frac {1}{3}}}\,dx=$	(auswerten)
$\int _{1}^{4}{\frac {x({\frac {2}{3}}x+{\frac {1}{3}})^{2}}{2}}-x^{2}({\frac {2}{3}}x+{\frac {1}{3}})+{\frac {({\frac {2}{3}}x+{\frac {1}{3}})^{3}}{3}}-({\frac {x({\frac {5}{3}}x-{\frac {11}{3}})^{2}}{2}}-x^{2}({\frac {5}{3}}x-{\frac {11}{3}})+{\frac {({\frac {5}{3}}x-{\frac {11}{3}})^{3}}{3}})\,dx=$	(ausmultiplizieren)
$\int _{1}^{4}{\frac {2}{9}}x^{3}+{\frac {2}{9}}x^{2}+{\frac {1}{18}}x-{\frac {2}{3}}x^{3}-{\frac {1}{3}}x^{2}+{\frac {8}{81}}x^{3}+{\frac {4}{27}}x^{2}+{\frac {2}{27}}x+{\frac {1}{81}}-{\frac {25}{18}}x^{3}+{\frac {55}{9}}x^{2}-{\frac {121}{18}}x+{\frac {5}{3}}x^{3}-{\frac {11}{3}}x^{2}-{\frac {125}{81}}x^{3}-{\frac {605}{27}}x+{\frac {1331}{81}}\,dx=$

Ich höre an dieser Stelle auf, weil die Wahrscheinlichkeit eines Rechen- oder Tippfehlers hier gegen 1 geht... (P(Fehler) --> 1)

Es geht genau so weiter wie oben auch...

Wolfram Alpha kommt auf folgendes Ergebnis (für den 2ten Teil):

$\int _{1}^{4}{\frac {148}{9}}-29x+{\frac {38x^{2}}{3}}-{\frac {29x^{3}}{18}}\,dx={\frac {-39}{8}}\approx -4,875...$