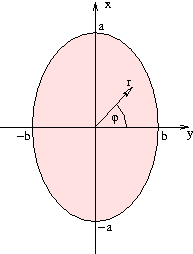
Berechnen Sie die Fläche einer Ellipse, deren Haupt- bzw. Nebenachse die Länge a bzw. b hat.
Hinweis: Benützen Sie die Trasformation x = a.r.cos(s) und y = a.r.sin(s)
Die komischen Nullen sind Thetas.
Datei:Newfile.pdf
x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1} y = b 1 − x 2 a 2 {\displaystyle y=b{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}} b ∫ − a a 1 − x 2 a 2 d x {\displaystyle b\int _{-a}^{a}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}dx} t = x a {\displaystyle t={\frac {x}{a}}} x = t a {\displaystyle x=ta} d x = a d t {\displaystyle dx=a\;dt} b ∫ − a a 1 − t 2 ∗ a d t = a b ∫ − a a 1 − t 2 d t {\displaystyle b\int _{-a}^{a}{\sqrt {1-t^{2}}}*adt=ab\int _{-a}^{a}{\sqrt {1-t^{2}}}dt} s = sin − 1 ( t ) {\displaystyle s=\sin ^{-1}{(t)}} t = sin ( s ) {\displaystyle t=\sin {(s)}} d t = cos ( s ) d s {\displaystyle dt=\cos {(s)}ds} a b ∫ − a a 1 − sin 2 ( s ) ∗ cos ( s ) d s {\displaystyle ab\int _{-a}^{a}{\sqrt {1-\sin ^{2}{(s)}}}*\cos {(s)}\;ds}
Fakt: cos ( s ) = 1 − sin 2 ( s ) {\displaystyle \cos {(s)}={\sqrt {1-\sin ^{2}{(s)}}}} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) − a b ∫ − a a − sin ( s ) ∗ sin ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}-ab\int _{-a}^{a}-\sin {(s)}*\sin {(s)}} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) − a b ∫ − a a − sin 2 ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}-ab\int _{-a}^{a}-\sin ^{2}{(s)}} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) + a b ∫ − a a sin 2 ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}+ab\int _{-a}^{a}\sin ^{2}{(s)}}
Fakt: sin 2 ( s ) = 1 − cos 2 ( s ) {\displaystyle \sin ^{2}{(s)}=1-\cos ^{2}{(s)}} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) + a b ∫ − a a 1 − cos 2 ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}+ab\int _{-a}^{a}1-\cos ^{2}{(s)}} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) + a b ∫ − a a 1 − a b ∫ − a a cos 2 ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}+ab\int _{-a}^{a}1-ab\int _{-a}^{a}\cos ^{2}{(s)}} 2 a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) + a b ∫ − a a 1 {\displaystyle 2ab\int _{-a}^{a}\cos ^{2}{(s)}=\cos {(s)}*\sin {(s)}+ab\int _{-a}^{a}1} a b ∫ − a a cos 2 ( s ) = cos ( s ) ∗ sin ( s ) + a b s 2 {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}={\frac {\cos {(s)}*\sin {(s)}+abs}{2}}} a b ∫ − a a cos 2 ( s ) {\displaystyle ab\int _{-a}^{a}\cos ^{2}{(s)}} 2 a b ∫ − a a cos 2 ( s ) {\displaystyle 2ab\int _{-a}^{a}\cos ^{2}{(s)}} s = sin − 1 ( t ) {\displaystyle s=\sin ^{-1}{(t)}} cos ( sin − 1 ( t ) ) ∗ sin ( sin − 1 ( t ) ) + a b sin − 1 ( t ) {\displaystyle \cos {(\sin ^{-1}{(t)})}*\sin {(\sin ^{-1}{(t)})}+ab\sin ^{-1}{(t)}}
Fakt: cos ( sin − 1 ( t ) ) = 1 − sin 2 ( sin − 1 ( t ) ) = 1 − t 2 {\displaystyle \cos {(\sin ^{-1}{(t)})}={\sqrt {1-\sin ^{2}{(\sin ^{-1}{(t)})}}}={\sqrt {1-t^{2}}}} 1 − t 2 ∗ t + a b sin − 1 ( t ) 2 {\displaystyle {\frac {{\sqrt {1-t^{2}}}*t+ab\sin ^{-1}{(t)}}{2}}} t = x a {\displaystyle t={\frac {x}{a}}} 1 − x 2 a 2 ∗ x a + a b sin − 1 ( x a ) 2 ∣ − a a = a b π 4 − ( − a b π 4 ) = a b π 2 {\displaystyle {\frac {{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}*{\frac {x}{a}}+ab\sin ^{-1}{({\frac {x}{a}})}}{2}}\mid _{-a}^{a}={\frac {ab\pi }{4}}-(-{\frac {ab\pi }{4}})={\frac {ab\pi }{2}}} 2 ∗ a b π 2 = a b π {\displaystyle 2*{\frac {ab\pi }{2}}=ab\pi } Blueroot 16:26, 15. Mai 2007 (CEST)
Ellipse Und hier noch die Kurzversion vom Großmeister Karigl:
x 2 a 2 + y 2 b 2 = 1 ⟹ ∬ E p i p s e 1 d x d y {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\quad \Longrightarrow \iint \limits _{Epipse}1\;dx\;dy}
Substitution in Polarkoordinaten:
x = a ⋅ r cos φ 0 ≤ φ ≤ 2 π y = b ⋅ r sin φ 0 ≤ r ≤ 1 } B {\displaystyle \left.{\begin{array}{ll}x=a\cdot r\cos \varphi &0\leq \varphi \leq 2\pi \\y=b\cdot r\sin \varphi &0\leq r\leq 1\end{array}}\right\}B}
mit der Funktionsdeterminante:
∂ ( x , y ) ∂ ( r , φ ) = | a cos φ b sin φ a ⋅ r ( − sin φ ) b ⋅ r cos φ | = a ⋅ b ⋅ r {\displaystyle {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}a\cos \varphi &b\sin \varphi \\a\cdot r(-\sin \varphi )&b\cdot r\cos \varphi \end{vmatrix}}=a\cdot b\cdot r}
(siehe auch Bsp.127b )
∬ B d x d y = ∫ 0 2 π ∫ 0 1 1 ⋅ a b r d r d φ = ∫ 0 2 π a b r 2 2 | 0 1 ⏟ a b 2 d φ = a b 2 ∫ 0 2 π d φ = a b 2 2 π = a b π {\displaystyle \iint \limits _{B}dx\;dy=\int \limits _{0}^{2\pi }\int \limits _{0}^{1}1\cdot abr\;dr\;d\varphi =\int \limits _{0}^{2\pi }\underbrace {\left.{\frac {abr^{2}}{2}}\right|_{0}^{1}} _{\tfrac {ab}{2}}d\varphi ={\frac {ab}{2}}\int \limits _{0}^{2\pi }d\varphi ={\frac {ab}{2}}2\pi =ab\pi }
--Baccus 12:54, 17. Mai 2007 (CEST)
Wikipädia: