TU Wien:Mathematik 2 UE (diverse)/Übungen SS07/Beispiel 127

Berechnen Sie das folgende Gebietsintegral:

$\iiint \limits _{Z}x\;dx\;dy\;dz$ , wobei $Z\subset \mathbb {R} ^{3}$ der Zylinder $Z=\left\{(x,y,z)|1\leq z\leq 2,1\leq x^{2}+y^{2}\leq 2\right\}$ ist.

Übungsgruppe Montag:

...mit Satz v. Fubini (d.h. ohne Substitution für Bereichsintegrale), und mit der Einheitskugel anstelle von Z.

Übungsgruppe Mittwoch:

a) ...mit Satz v. Fubini (d.h. ohne Substitution für Bereichsintegrale),

b) ...mit Substitution.

Hilfreiches[Bearbeiten | Quelltext bearbeiten]

Vorlage:Gebietsintegral

Satz von Fubini

Satz von Fubini[Bearbeiten | Quelltext bearbeiten]

Sei $B=\{(x,y)\in \mathbb {R} ^{2}|\varphi (y)\leq x\leq \psi (y),c\leq y\leq d\}$ , wobei $\phi (y)$ und $\psi (y)$ zwei stetige Funktionen sind. Dann gilt $\int \int _{B}f(x,y)\,dx\,dy=\int _{c}^{d}\int _{\varphi (y)}^{\psi (y)}f(x,y)\,dx\,dy$

Wikipedia

Lösungsvorschlag von Baccus (Mittwoch, "Zylinder")[Bearbeiten | Quelltext bearbeiten]

a) Fubini[Bearbeiten | Quelltext bearbeiten]

(Vorsicht: Das ist eine Lösung für faule Leute (=mich): man kommt ohne jegliches Integrieren aus! :-))

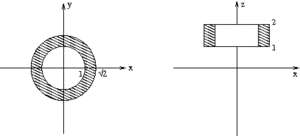
Die Figur ist ein Hohlzylinder; wir berechnen also zuerst den äußeren, größeren Zylinder ( $Z_{1},\;r={\sqrt {2}}$ ), und ziehen den kleineren, inneren Zylinder ( $Z_{2},\;r=1$ ) davon ab: $Z=Z_{1}-Z_{2}$ . Soweit der Plan.

$Z_{1}=\int \limits _{1}^{2}\int \limits _{-{\sqrt {2}}}^{\sqrt {2}}\int \limits _{-{\sqrt {2-y^{2}}}}^{\sqrt {2-y^{2}}}x\;dx\;dy\;dz$

Die Reihenfolge der Auswertung des Mehrfach-Integrals kann man beliebig wählen (und die Berechnung damit beliebig kompliziert zu gestalten); ich habe mich dazu entschieden, $\int \ldots dx$ zuerst zu berechnen.

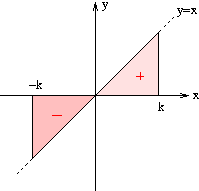
Das innerste Integral ist also $\iint \underbrace {\left(\int \limits _{-k}^{k}x\;dx\right)} _{0}dy,z$

Aus der graphischen Abschätzung der inneren Funktion y=x (Skizze) folgt, daß die beiden Dreiecksflächen equiplanar und einmal negativ, einmal positiv sind: in Summe Null.

Da somit schon das innerste Integral ( $\int _{-k}^{k}x\;dx$ ) Null ergibt, erübrigt sich die Berechnung der weiteren (äußeren) Integrale; $\iint 0=0$ .

Damit wird auch die weitere Berechnung des Zylinders $Z_{2}$ und von $Z=Z_{1}-Z_{2}$ obsolet, das Ergebnis ist jedenfalls Null.

b) Substitution[Bearbeiten | Quelltext bearbeiten]

Substitution in Polar- (bzw. Zylinder-)koordinaten (+ Grenzen):

$\underbrace {\begin{array}{ll}x=r\cdot \cos \varphi &1\leq r\leq {\sqrt {2}}\\y=r\cdot \sin \varphi &0\leq \varphi \leq 2\pi \\z=s&1\leq s\leq 2\end{array}} _{\doteq K}$

Für die Substitution müssen die Integrations-Domänen neu bestimmt werden ( $\rightarrow$ Determinante der Funktionsmatrix):

$dx\;dy\;dz={\begin{vmatrix}x_{r}&x_{\varphi }&x_{s}\\y_{r}&y_{\varphi }&y_{s}\\z_{r}&z_{\varphi }&z_{s}\\\end{vmatrix}}dr\;d\varphi \;ds$

${\begin{vmatrix}\cos \varphi &-r\cdot \sin \varphi &0\\\sin \varphi &r\cdot \cos \varphi &0\\0&0&1\end{vmatrix}}=r\cdot \cos ^{2}\varphi +r\cdot \sin ^{2}\varphi =r\cdot \underbrace {(\cos ^{2}\varphi +\sin ^{2}\varphi )} _{1}=r$

Damit erhalten wir

$\iiint \limits _{K}r\cdot \cos \varphi \cdot r\;dr\;d\varphi \;ds=$

(Die Reihenfolge der Auswertung des Mehrfach-Integrals ist beliebig wählbar; nachdem das aber auch eine Lösung für faule Leute werden soll (ich ziehe allerdings den Ausdruck "Weg des geringsten Widerstandes" vor :-)), wählen wir $d\varphi$ ):

$\iint \underbrace {\left(\int \limits _{0}^{2\pi }r^{2}\cdot \cos \varphi \;d\varphi \right)} _{r^{2}\sin \varphi |_{0}^{2\pi }=0}dr,s$

Der Sinus ist an beiden Grenzen =0, das innerste Integral also (auch wieder) Null. Damit ersparen wir uns die Berechnung der äußeren Integrale, das Ergebnis ist (w.o.) Null.

Anmerkung[Bearbeiten | Quelltext bearbeiten]

Auf Grund einiger Zweifel hinsichtlich des Ergebnisses im Informatik-Forum:

Das Ergebnis wurde in beiden Varianten genau so von Prof Urbanek vorgerechnet und das Ergebnis ist in beiden Fällen null. Eigentlich logisch, da nur das Integral und nicht das Volumen berechnet werden soll. Und die Kreishälften über und unter der x-Achse heben sich gegenseitig auf, also ist der Wert des Integrals tatsächlich 0. Und wenn man zuerst das innerste Integral berechnet, sind alle weiteren Ergebnisse ebenfalls null.

Hapi