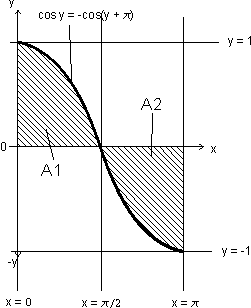TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 157
Angabe[Bearbeiten | Quelltext bearbeiten]
Berechnen Sie das Gebietsintegral: ist das Quadrat mit den Eckpunkten , , , .
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Nicht ganz korrekter Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Nicht ganz korrekter Lösungsvorschlag, welcher die Flächen ober- und unterhalb der x-Achse einfach zusammenzählt und dadurch "nivelliert".
Zwischenschritt:
Korrekter Lösungsweg[Bearbeiten | Quelltext bearbeiten]
Die Integration im "inkorrekten Lösungsweg stimmt, bis auf die Grenzen. Betrachten wir . Wir schauen uns die Cosinuskurve im Bereich der Integrationsgrenzen an:
Wir müssen nun die Gesamtfläche durch ( ist negativ) berechnen, siehe auch diesen Link.
Somit müssen wir wie folgt integrieren:
Kontrolle mit MATLAB (symbolic toolbox)[Bearbeiten | Quelltext bearbeiten]
>> syms x y;
>> f=sin(x+y);
>> F=int(f,x,0,pi)
F =
2*cos(y)
>> Fe = int(F,y,0,pi/2)
Fe =
1
usw.
Anmerkung von Sonni[Bearbeiten | Quelltext bearbeiten]
Aufgabenstellung war das Integral zu berechnen und nicht das Volumen. Somit ist der "Nicht ganz korrekte Lösungsvorschlag" korrekter als der "Korrekte Lösungsweg". In zweiterem nehmen wir den Bereich A2 betragsmäßig in die Summe, was jedoch nur bei Volumenberechnungen gemacht werden darf. Ich danke für diese Aufklärung der Tutorin Elisabeth Fink.
Links[Bearbeiten | Quelltext bearbeiten]
Ähnliche Beispiele:
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 158
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 159
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 160
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 161
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 162
- TU Wien:Mathematik 2 UE (diverse)/Übungen WS07/Beispiel 163
Websites[Bearbeiten | Quelltext bearbeiten]
Informatikforum[Bearbeiten | Quelltext bearbeiten]
- Aktueller Thread --Markus Nemetz 11:50, 12. Mai 2006 (CEST)
- UE Runde 8 (18.05.06), Gruppe 12, Allg. Tipps --Markus Nemetz 06:27, 11. Mai 2006 (CEST)
Andere Websites[Bearbeiten | Quelltext bearbeiten]
- Integral von Sinus --Markus Nemetz 20:54, 11. Mai 2006 (CEST)
- Online Integrator --Markus Nemetz 20:54, 11. Mai 2006 (CEST)
- DoppelintegraleSuperlufti 16:54, 16. Mai 2006 (CEST)
- Integrale über Rechteckige Bereiche ----Superlufti 08:13, 17. Mai 2006 (CEST)
Quelle[Bearbeiten | Quelltext bearbeiten]
Panholzer Beispielsammlung SS06 Beispiel 62 / SS07 Beispiel 124