Man berechne:

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Betrachten wir ein rechtwinkeliges Dreieck mit dem Winkel  , der Ankathete
, der Ankathete  und der Gegenkathete
und der Gegenkathete  .
.
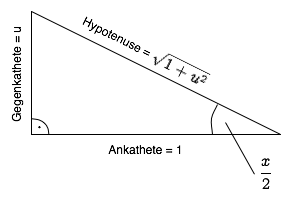
Dabei ergibt sich folgendes:



Wir substituieren also  .
.
(Anmerkung von koDiacc (da ich persönlich ewig gebraucht habe, um diesen Teil nachzuvollziehen: http://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Gegenseitige_Darstellung dort wird erklärt wie man den sin anhand von tangens ausdrücken kann. da wir aber sin x/2 haben muss ich eben tan x auch durch tan x/2 aufschreiben. dieses tan x/2 ersetze ich dann durch u))
Das Additionstheorem für die Sinusfunktion besagt folgendes:

In unserem Fall:

Abgeleitet



(2. Anm. v. koDiacc: (tan x)' = 1/cos^2 x d.h. tan x/2 muss ich das x/2 substituieren und dann kettenregel somit steht dann 1/2 davor)
Nun können wir das Integral folgendermaßen anschreiben:

Rücksubstituieren:

SS07 Beispiel 51
