Wie ist t {\displaystyle t} f ( x ) = ( x 2 + t ) / ( x − t ) {\displaystyle f(x)=(x^{2}+t)/(x-t)} x 0 = 1 {\displaystyle x_{0}=1}
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Quotientenregel ( f g ) ′ = f ′ g − f g ′ g 2 {\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}
Theoretisches: Die erste Ableitung einer Funktion entspricht der Steigung. Eine streng monoton fallende Funktion hat eine negative Steigung.
Keine Garantie auf das hier!!!
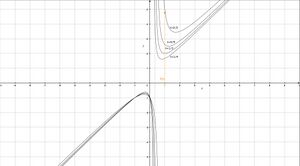
Skizze für die Lösung t>1/3 Angabe:
f ( x ) = ( x 2 + t x − t ) {\displaystyle f\left(x\right)=\left({\frac {x^{2}+t}{x-t}}\right)\;}
( f g ) ′ = f ′ ⋅ g − f ⋅ g ′ g 2 {\displaystyle \left({\frac {f}{g}}\right)^{'}={\frac {f\;'\cdot g\;-\;f\cdot g'}{g^{2}}}}
f und g:
f = x 2 + t {\displaystyle f=x^{2}+t}
f ′ = 2 x {\displaystyle f'=2x}
g = x − t {\displaystyle g=x-t}
g ′ = 1 {\displaystyle g'=1}
Ableitung bilden:
2 x ( x − t ) − ( x 2 + t ) ( x − t ) 2 = {\displaystyle {\frac {2x\;\left(x-t\right)\;-\;\left(x^{2}+t\right)}{\left(x-t\right)^{2}}}=}
= 2 x 2 − 2 x t − x 2 − t ( x − t ) 2 {\displaystyle ={\frac {2x^{2}\;-\;2xt\;-\;x^{2}\;-\;t}{\left(x-t\right)^{2}}}}
für x0=1 :
x 0 = 1 ; {\displaystyle x_{0}=1;\;}
1 − 2 t − t ( 1 − t ) 2 < 0 {\displaystyle {\frac {1-2t-t}{\left(1-t\right)^{2}}}\;<\;0\;}
1 − 3 t < 0 {\displaystyle \;1-3t\;<\;0\;}
t > 1 3 {\displaystyle \;t\;>\;{\frac {1}{3}}\;}
Wenn t>1/3 ist, ergibt sich ein negatives Ergebnis der 1. Ableitung im Punkt x0=1. Daher streng monoton fallend.
Beispiel für Graphen aus der Skizze: y = ( x 2 + ( 4 9 ) ( x − 4 9 ) ) {\displaystyle y=\left({\frac {x^{2}+\left({\frac {4}{9}}\right)}{\left(x-{\frac {4}{9}}\right)}}\right)}
Anmerkung von fallingcats :
Die Ungleichung
1 − 2 t − t ( 1 − t ) 2 < 0 {\displaystyle {\frac {1-2t-t}{\left(1-t\right)^{2}}}\;<\;0\;} zwei Lösungen :
1 3 < t < 1 {\displaystyle {\frac {1}{3}}<t<1\;} t > 1 {\displaystyle \;t>1}
Eine davon vor der Nullstelle bei t=1, eine danach.