TU Wien:Parallel Computing VU (Träff)/Zusammenfassung
Introduction[Bearbeiten | Quelltext bearbeiten]
Processor performance is defined as the maximum number of operations that can be carried out per unit of time. Often FLoating point OPerations per Second (FLOPS).
Parallel Computing is intimately related to distributed and concurrent computing:
- Parallel Computing
- Efficiently utilizing dedicated parallel resources for solving given computation problems.
- Distributed Computing
- Making independent, non-dedicated resources available and cooperate toward solving specified problem complexes.
- Concurrent Computing
- Managing and reasoning about interacting processes that may or may not progress simultaneously.
For designing and analyzing parallel algorithms, a suitable model is needed. A good model is a bridging model (if an algorithm performs better in the model, a faithful implementation of it also performs better).
A bridging model for sequential computing is the RAM, Random Access Machine.
PRAM model[Bearbeiten | Quelltext bearbeiten]
While the Parallel Random Access Machine (PRAM) model is unrealistic it is extremely useful.
- Assumes as large as needed memory
- Processors can read/write into memory in unit time (uniform memory access, UMA)
- Number of processors can be chosen as convenient
- Processors execute their own program
- Processors are strictly synchronized (operating in lock-step)
The PRAM model defines what happens when multiple processors access the same memory word in the same step:
- EREW (Exclusive Read Exclusive Write)
- CREW (Concurrent Read Exclusive Write)
- CRCW (Concurrent Read Concurrent Write)
- Common CRCW: writing processors must write the same value
- Arbitrary CRCW: either of the written values will survive
- Priority CRCW: processor with the highest priority will successfully write
- Theorem 1
- The maximum of n numbers stored in an array can be found in parallel time steps, using processors (and performing operations) on a Common CRCW PRAM.
- Theorem 2
- The maximum of n numbers stored in an array can be found in parallel time steps, using a maximum of n/2 processors (but performing only operations) on a CREW PRAM.
- Theorem 3
- Two n × n matrices can be multiplied into a matrix C in time steps and operations on an EREW PRAM.
Flynn's taxonomy[Bearbeiten | Quelltext bearbeiten]
Flynn's taxonomy looks at the instruction stream(s) and the data stream(s) of the system:
- SISD (single instruction, single data), e.g. sequential computer
- SIMD (single instruction, multiple data), e.g. single instruction operates on a larger batch of data
- MISD (multiple instruction, single data), e.g. pipelined system
- MIMD (multiple instruction, multiple data), e.g. PRAM machine
SPMD (same program, multiple data) is a subcase of MIMD.
Performance and objectives[Bearbeiten | Quelltext bearbeiten]
- absolute speed-up
- The absolute speed-up of parallel algorithm Par over sequential algorithm Seq for input of size O(n) on p processor-cores is the ratio of sequential to parallel running time, i.e.,
- relative speed-up
- The relative speed-up of a parallel algorithm Par is the ratio of the running time with one processor-core to the parallel running time with p processor-cores, i.e.,
- Amdahl's Law
- Assume that the work performed by sequential algorithm Seq can be divided into a strictly sequential fraction s, 0 < s ≤ 1, independent of n, that cannot be parallelized at all, and a fraction r = ( 1 − s ) that can be perfectly parallelized. The parallelized algorithm is Par. The maximum speed-up that can be achieved by Par over Seq is 1/s.
- strongly scalable
- The parallel time decreases proportionally to p (linear speed-up), while keeping n constant.
- weakly scalable
- The parallel running time remains constant, while keeping the average work per processor constant and increasing n.
Patterns and paradigms[Bearbeiten | Quelltext bearbeiten]
The work required to solve some problem on given input size n by some algorithm can be described as a set of smaller tasks to be executed in some order. The dependencies between these tasks can be modeled as directed edges in a directed acyclic graph (DAG).
: number of sequential operations required for task
Ignoring communication costs total work is .
is the sequential part of any DAG (fastest possible parallel execution with unlimited number of processors).
- Work Law
- Depth Law
Merging problem[Bearbeiten | Quelltext bearbeiten]
Merge two ordered sequences.
- merging by ranking
- merging by co-ranking
Prefix sums[Bearbeiten | Quelltext bearbeiten]
Given an array and an associative operator , compute
- inclusive prefix-sum
- or exclusive prefix-sum
- load balancing with prefix-sums
- recursive prefix-sums
- solving recurrences with the Master Theorem
- iterative prefix-sums
- non work-optimal, faster prefix-sums
- blocking
[Bearbeiten | Quelltext bearbeiten]
A naive, parallel shared-memory system model:
- A (fixed) number of processor-cores p connected to a large (but finite) shared memory.
- Every core can read/write every location in memory, but memory access is significantly more expensive than performing operations in the processor-core.
- memory accesses are not uniform, from each processors point of view some locations can be accessed (much) faster than other locations.
- Processors are not synchronized.
All these assumptions are in stark contrast to those made for the idealized #PRAM model.
Caches[Bearbeiten | Quelltext bearbeiten]
The cache system of a standard processor does not work on the granularity of single words in memory, but on larger blocks of memory addresses. The memory can be thought of as being segmented into small blocks (typically 64 bytes) and each block can be mapped to some cache line.
There are different ways how memory blocks can be mapped to cache lines:
- directly mapped: each block is mapped to one predetermined cache line
- fully associative: each block can be mapped to any cache line
- k-way set associative: each block can be mapped to some predetermined, small set of cache lines (set size = k)
When a processor reads a word and the memory block to which the block belongs is in the cache, we have a cache hit. Otherwise we have a cache miss, and the block has to be read from slow memory. There are three types of cache misses:
- compulsory (cold) miss: the cache is empty
- capacity miss: the cache is full
- conflict miss: all cache lines where the block can fit are occupied (can only happen for directly and set associative)
In a k-way set associative cache, either of the k cache lines can be evicted upon a conflict miss. Typically used replacement policies are least recently used (LRU) and least frequently used (LFU).
On a write to memory:
- if the block is cached, the cache must be updated
- if the block is not cached, it can be cached (write allocate) or not (write no-allocate)
When the cache is updated, the memory can be updated immediately (write-through), or the updating of the memory can be postponed until the cache line is evicted (write back).
Such a cache system can benefit applications/algorithms in two ways:
- temporal locality: memory address is reused frequently (will not be evicted)
- spatial locality: addresses of the same block are also used
Matrix-matrix multiplication[Bearbeiten | Quelltext bearbeiten]
Access locality matters; a standard, and highly illustrative example application is the matrix-matrix multiplication.
- Matrix multiplied with Matrix
- sequential algorithm in or (for squares)
- three loops (for ) can be parallelized, order of parallelization matters
- differences because matrices are accessable in row order
- different index order causes more or fewer cache misses
- Recursive matrix-matrix multiplication algorithm
- recursively split and in smaller submatrices until very small then iterative solution
- Blocked matrix-matrix multiplication
- split matrices into blocks at start
- then multiply with 6 nested loops
- block size can be chosen depending on cache size
- called cache-aware algorithm (opposite is cache-oblivious)
Multi-core caches[Bearbeiten | Quelltext bearbeiten]
- cache system has several dimensions
- L1 (lowest level) to L3 (or more)
- L1 is closest to processor, smallest (few KB) and fastest
- L3 is Last Level Cache LLC, several MB big
- L1 has data and instruction cache
- Translation Lookaside Buffer for memory management (pages)
- lowest level caches are private (only for one processor)
- higher level caches are shared
Caches in parallel multi-core systems pose new problems:
- cache coherence problem
- when one block is updated in one cache and also stored in another cache of another processor
- coherent cache system if line of other cache will be updated at some point in time (can also just mean it is invalidated in the cache)
- non coherent if it will never be updated
- problem solved through cache coherence protocol, may cause a lot of cache coherence traffic
- false sharing
- when two caches have the same blocks of memory stored
- update to one address of block will cause the whole line of other to be replaced
The memory system[Bearbeiten | Quelltext bearbeiten]
- cache system part of memory hierarchy
- from fast low levels (caches) to slower bigger higher levels
- write buffer for memory writes (FIFO)
- for multi-core CPUs not every processor has direct connection to main memory
- instead connected to memory controller
- some processors closer to memory controller than others address access times are not uniform
Super-linear speed-up[Bearbeiten | Quelltext bearbeiten]
- through memory hierarchy of large caches, working sets of each processor get smaller and eventually can fit into the fastest caches
Application performance[Bearbeiten | Quelltext bearbeiten]
- memory-bound: the operations to be performed per memory access take less time than the memory access
- compute-bound: the operations to be performed per memory access take more time than the memory access
Memory consistency[Bearbeiten | Quelltext bearbeiten]
- when process 1 sets a certain flag in memory and process 2 checks if that flag is set it may happen that the flag is still in the write buffer and process 2 may read a wrong value
- programming interfaces like
pthreadsandOpenMPprovide constructs to ensure a well-defined memory state at certain points
pthreads[Bearbeiten | Quelltext bearbeiten]
A thread is the smallest execution unit that can be scheduled.
The main characteristics of the pthreads programming model are:
- Fork-join parallelism. A thread can spawn any number of new threads (up to system limitations) and wait for completion of threads. Threads are referenced by thread identifiers.
- Threads are symmetric peers, any threads can wait for completion of any other thread via the thread identifier.
- One initial main thread
- SPMD but can be MIMD
- Threads are scheduled by the OS
- No implicit synchronization
- Threads in a process share global information
- Coordination constructions for synchronization and updates to shared objects
pthreads in C[Bearbeiten | Quelltext bearbeiten]
- include header
#include <pthread.h> - compile with gcc flag
-pthread
Race conditions[Bearbeiten | Quelltext bearbeiten]
- race condition
- When e.g. two threads update a variable at the same time, outcome may be write of either thread → non-deterministic result.
- data race
- Two or more threads access a shared object, at least one of those accesses is a write.
Critical sections, MutEx, locks[Bearbeiten | Quelltext bearbeiten]
A lock is programming model to guarantee mutual exclusion on a critical section.
- threads try to acquire lock, if granted they enter critical section, release lock when done
- threads are blocked till lock is acquired
- deadlock free
- If any number of threads are trying to acquire the lock, eventually one thread must succeed.
- starvation free
- Any specific thread trying to acquire the lock will eventually acquire it, no matter which other threads are also trying to acquire the lock.
In pthreads a lock is called a mutex. pthreads mutex'es guarantee mutual exclusion and are deadlock free, but not starvation free.
- threads at lock will serialize, one thread after another will pass critical section
- locks where many threads are competing are called contended
- try-locks allow execution of some code when lock could not be acquired
Waiting for a lock can be implemented in two ways:
- with a spin-lock the core executing the blocked thread actively keeps testing (spinning) for the lock to become free
- with a blocking lock the blocked thread is suspended by the OS, the core is free to do something else
(may be advantageous when the shared-memory system is oversubscribed)
In pthreads, spinning behavior can be requested explicitly by using spin locks.
- condition variables are associated with mutex
- thread waits on variable till a signal occurs
- a thread can signal one (maybe arbitrary) thread only
- a broadcast signals all threads at once
- concepts with conditions with signals and waits are called monitor
- barriers are similar to mutex with conditions
- concurrent initialization is where first thread executes initialization code before other threads begin
Locks in data structures[Bearbeiten | Quelltext bearbeiten]
- trivially make data structures work with parallel algorithms by using a single lock for all operations on structures
- other way is to construct concurrent data structures
Problems with locks[Bearbeiten | Quelltext bearbeiten]
- deadlocks can happen easily with locks
- can also happen when the same thread tries to acquire same lock again
- locks around long critical section cause harmful serialization
- threads crashing during critical section also cause deadlocks
- threads can starve
- priority threads and locks can lead to lower priority threads preventing higher priority threads from continuing
Atomic operations[Bearbeiten | Quelltext bearbeiten]
- atomic instruction carry out instructions that cannot be interfered with by other threads
a = a+27can be implemented as atomic instruction throughfetch-and-add- crashing threads during atomic instructions will not cause deadlocks
- instructions are wait-free because they always execute in
- instructions are lock-free if any thread will be able to execute instruction in a bounded amount of time (not always given)
OpenMP[Bearbeiten | Quelltext bearbeiten]
The main characteristics of the OpenMP programming model are:
- Parallelism is (mostly) implicit through work sharing. All threads execute the same program (SPMD).
- Fork-join parallelism: Master thread implicitly spawns threads through parallel region construct, threads join at the end of parallel region.
- Each thread in a parallel region has a unique integer thread id, and threads are consecutively numbered from 0 to the number of threads minus one in the region.
- The number of threads can exceed number of the processors/cores. Threads intended to be executed in parallel by available cores/processors.
- Constructs for sharing work across threads. Work is expressed as loops of independent iterations and task graphs.
- Threads can share variables; shared variables are shared among all threads. Threads can have private variables.
- Unprotected, parallel updates of shared variables lead to data races, and are erroneous.
- Synchronization constructs for preventing race conditions.
- Memory is in a consistent state after synchronization operations.
The OpenMP specifications are available online (but you only need to know what is discussed in the lecture).
OpenMP in C[Bearbeiten | Quelltext bearbeiten]
- include header
#include <omp.h> - compile with gcc flag
-fopenmp
Parallel regions[Bearbeiten | Quelltext bearbeiten]
The parallel construct starts parallel execution.
There is an implicit barrier at the end of the parallel construct.
#pragma omp parallel [clauses]
{
// threads
}
where clauses is a comma-separated list of:
num_threads(t)
- If this clause is not given the default number of threads is used. The default can be set with the
omp_set_num_threads(t)library function or theOMP_NUM_THREADSenvironment variable.
- one or multiple #Sharing clauses
Sharing clauses[Bearbeiten | Quelltext bearbeiten]
Per default, all variables declared before a parallel region are shared by the threads in the region. Variables declared in the structured block of the parallel region are private.
Sharing of variables can be controlled with the following clauses:
default(shared|none)
Whether variables are shared by default or not.private(<vars>)
Make uninitialized copies of the listed variables.firstprivate(<vars>)
Makes copies of the listed variables and initializes each copy to the value the variable had before the parallel region.shared(<vars>)
It is good practice to not share variables by default by settingdefault(none)and explicitly listing the variables to be shared with theshared()clause.
Shared variables make data races possible.
Worksharing constructs[Bearbeiten | Quelltext bearbeiten]
Loop construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp for [clauses...] for (loop range...)
- loop scheduling is assignment of iteration blocks to threads
- each iteration has to be executed exactly once
- data races have to be avoided
For loops must be in canonical form:
- all threads must have same start and end values for i and same step
- loop ranges have to be finite and determined (no while loops possible)
- end condition has to be in the form of:
i<n, i<=n, i>n, i>=n, i!=n, with n as an expression or value - steps have to be in form of
i++, i--, i+=inc, i=i+inc, i-=inc, i=i-inc
#pragma omp parallel for [clauses...]
- shorthand for parallel region with one loop
- next statement is for loop
- always barrier after
Loop scheduling[Bearbeiten | Quelltext bearbeiten]
- how is each thread assigned to each iteration
- loop range is divided in consecutive chunks
- static schedule: chunks have same size and are assigned like round-robin (each thread gets chunk one after another)
- computation of chunk assignments is very fast (low overhead)
- dynamic: each thread dynamically grabs next chunk it can
- guided: dynamic assignment but chunk size changes, determined by number of iterations divided by threads
- set like
schedule(static|dynamic|guided[, chunksize])- for guided
chunksizeis minimum size - if no size given then default size is used
- for guided
- also possible
schedule(auto|runtime)- runtime: scheduling is set at runtime
- auto: OpenMP compiler determines
Collapsing nested loops[Bearbeiten | Quelltext bearbeiten]
- transform multiple loops into one
#pragma omp parallel for collapse(depth) [clauses...]
- depth is the amount of nested loops to be parallelized
sections construct[Bearbeiten | Quelltext bearbeiten]
The code is split into small pieces that can be executed in parallel by available threads.
#pragma omp sections
- outer structure
- end of block is implicit barriers
- nowait possible
- variables can be designated (first)private
#pragma omp section
- marks an independent code section
- which thread executes which section is designated by runtime system
- best case: each thread executes a section, all threads run in parallel
task construct[Bearbeiten | Quelltext bearbeiten]
Tasks are very much like OpenMP Sections, but Sections are static, that is, the number of sections is set when you write the code, whereas Tasks can be created anytime, and in any number, under control of your program's logic.[1]
#pragma omp task [clauses...]
- task is like a function call
- completion of task may not happen immediately
- at latest when completion is requested (e.g. at end of parallel region)
- tasks can access any variables of the thread
- if those variables are changed in the task data races may occur
- task can be designated final and thus not generate any additional tasks
single construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp single
- statement is executed by either one of the threads
- other threads will wait at end of statement until all threads have reached end
- can be eliminated by
nowaitclause aftersingle- might cause race conditions
- allows making variables private or firstprivate (unlike master construct)
Master and synchronization constructs[Bearbeiten | Quelltext bearbeiten]
master construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp master
- declares statement to be executed by master thread only (thread id of 0)
- other threads will simply skip
barrier construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp barrier
- no thread can continue until all threads have reached barrier
critical construct[Bearbeiten | Quelltext bearbeiten]
pragma omp critical [(name)]
- threads will wait and only one thread will execute code of critical section
- section can have name
- shared variables can be updated by task in critical region
atomic construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp atomic [read|write|update|capture]
- for simple critical sections
- allow fetch and add (FAA) atomic operations
- update is
x++, x = x op ..., ... - capture is
y = x++, ...
taskwait construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp taskwait [depend(...)]
- wait for completion of generated tasks
- only dependency clause allowed
ordered construct[Bearbeiten | Quelltext bearbeiten]
#pragma omp ordered
- loops with dependency patterns that cannot be handled normally can be marked as ordered
- only one possible ordered block in a parallel loop
- other parts of iteration can still be performed in parallel
Library calls[Bearbeiten | Quelltext bearbeiten]
omp_get_thread_num(void)returns thread idomp_get_num_threads(void)returns number of threadsomp_get_max_threads(void)returns maximum possible threadsomp_set_num_threads(int num_threads)sets maximumomp_get_wtime(void)returns wall clock time in secondsomp_get_wtick(void)returns tick resolution of timer
Reductions[Bearbeiten | Quelltext bearbeiten]
#pragma omp for reduction(operator: variables)
- is clause of
for - operators are `+ - * & | ^ && || min max`
Locks[Bearbeiten | Quelltext bearbeiten]
- locks don't have condition variables
- recursive (nested) locks are possible in OMP
Special loops[Bearbeiten | Quelltext bearbeiten]
- OMP can try to utilize vector operations (SIMD)
#pragma omp simd [clauses...]
- followed by canonical for loop
- one thread executes loop but with SIMD instructions
#pragma omp for simd [clauses...]
- followed by canonical for loop
- loop executed by multiple threads
- each chunk executed with SIMD instructions
#pragma omp parallel for simd [clauses...]
- same as previous but with parallel region declared
#pragma omp taskloop [clauses...]
- recursively break iteration range into smaller ranges
- smaller ranges are then executed as tasks
- should be initiated by a single thread
- size of range can be adjusted by
grainsize()
Distributed memory systems[Bearbeiten | Quelltext bearbeiten]
Network properties: structure and topology[Bearbeiten | Quelltext bearbeiten]
- distributed memory introduces interconnection network (or interconnect)
- entities (cores, multi-core CPUs or larger systems) are connected through links (in any form)
A network without switches is called a direct network, a network with switches an indirect network.
- the topology of network can be modeled as an unweighted graph
- each node is a network communication element
- each edge denotes a direct link between two elements
- communication networks are mostly bidirected (represented as undirected graph)
- graph diameter is longest shortest path between two nodes
- is a lower bound on communication steps between two elements
- graph degree is maximum degree of all nodes
- bisection width is minimum number of edges to remove so that graph is partitioned into two equally large subsets
- worst possible networks are linear processor array and processor ring
- tree networks are binary or k-ary trees
- have
- d-dimensional mesh networks
- processors are identified by their integer vectors
- special case is torus network where edges wrap around
- hypercube network is special case of torus network
- modern systems often built as torus networks with 3 to 6 dimensions, called multi-stage networks
Communication algorithms in networks[Bearbeiten | Quelltext bearbeiten]
- unidirectional communication if only one direction
- bidirectional if in both directions can be communicated
- most modern systems
- broadcast problem: how to transmit data from root to every other node in minimal communication steps
- lower bound is in -degree, network with nodes
- algorithm to solve partitions network in smaller networks, root sends data to “virtual roots” of these networks, solve problem for smaller subnetworks
Communication costs[Bearbeiten | Quelltext bearbeiten]
- linear transmission cost assumes time of , where is start up latency and is time per unit of data
Routing and switching[Bearbeiten | Quelltext bearbeiten]
- if network is not fully connected, routs make path between two nodes possible
Hierarchical, distributed memory systems[Bearbeiten | Quelltext bearbeiten]
- communication networks with different levels
- processors may have different characteristics and thus live on different compute nodes
Programming models[Bearbeiten | Quelltext bearbeiten]
- concrete network properties are abstracted
- model of fully connected network
- processes are not synchronized and communicate with others through explicit or implicit transmission
- message transmission is assumed to be deadlock free and correct
- distributed system programming models either:
- data distribution centric: data structures distributed according to rules, if one processes changes data structure of another process then through communication
- communication centric: focuses on explicit communication and synchronization instead of data structures (MPI)
Message-Passing Interface[Bearbeiten | Quelltext bearbeiten]
- message-passing programming model is to structure parallel processes through sending and receiving messages
- the message-passing model is called Communicating Sequential Processes (CSP). CSP programs cannot have data races.
The main characteristics of the MPI message-passing programming model are:
- Finite sets of processes (in communication domains) that can communicate.
- Processes identified by rank in communication domain.
- Ranks successive ; p number of processes in domain (size).
- More than one communication domain possible; created relative to default domain of all started processes. A process can belong to several communication domains.
- Processes operate on local data, all communication explicit.
- Communication reliable and ordered.
- Network oblivious
- Three basic communication models:
- Point-to-point communication, different modes, non-local and local completion semantics
- One-sided communication, different synchronization mechanisms, local completion mechanisms
- Collective operations, non-local (and local) completion semantics.
- Structure of communicated data orthogonal to communication model and mode.
- Communication domains may reflect physical topology.
The MPI specifications are available online (but you only need to know what is discussed in the lecture).
The rest of this section is about MPI in C:
- header
#include <mpi.h> - functions in
MPI_“name space” (illegal and punishable by law to use prefix for own functions) MPI_SUCCESSreturn value for success (obviously)mpicccompiler to compile programs
Initializing MPI[Bearbeiten | Quelltext bearbeiten]
MPI_Initto initialize- end with
MPI_Finalize MPI_Abortforces termination in case of emergency
Error checking[Bearbeiten | Quelltext bearbeiten]
- MPI only has limited error checking because it is expensive
Communicators[Bearbeiten | Quelltext bearbeiten]
Communication domains are called communicators in MPI.
A communicator is a distributed object that can be operated upon by all
processes belonging to the communicator. A communicator is referenced
by a handle of type MPI_Comm.
MPI_Comm_sizeto get amount of processes in communicatorMPI_Comm_rankto get rank in communicator- all processes are in communication domain
MPI_COMM_WORLD MPI_Comm_splitsplits processes of communicator into smaller groups with own communicatorsMPI_Comm_createalso creates new communicators- both functions are collective (have to be called by all processes)
MPI_Comm_freeto free communicators
Organizing processes[Bearbeiten | Quelltext bearbeiten]
- communicator with grid structure is called Cartesian communicator
- created through
MPI_Cart_createreorderflag to reorder ranks so neighboring processes are close on grid
MPI_Cart_coordstranslate rank to coordinate vectorMPI_Cart_rankvice versa
Objects and handles[Bearbeiten | Quelltext bearbeiten]
- a distributed object is an object for which all processes that reference it can access it
- distributed objects
MPI_Commfor communicator objectMPI_Winfor communication windows
- local objects
MPI_Datatypefor local layout and structure of dataMPI_Groupfor ordered sets of processesMPI_Statusfor communicationMPI_Requestfor open (not yet completed) communicationMPI_Opfor binary operatorsMPI_Infofor additional info when creating objects
Process groups[Bearbeiten | Quelltext bearbeiten]
- objects of type
MP_Group - groups used locally by processes to order processes
MPI_Comm_groupreturns an ordered group from a communicatorMPI_Group_(size|rank)likeMPI_Comm_(size|rank)- set-like operations on groups possible,
MPI_Group_(union|intersection|difference|incl|excl...)
Point-to-point communication[Bearbeiten | Quelltext bearbeiten]
MPI_Sendto send data from process todestMPI_Recvto receive data fromsource- combined operations
MPI_Sendrecv[_replace]have argument forsourceanddest MPI_Get_(count|elements)to figure how much data was sent
Semantic terms[Bearbeiten | Quelltext bearbeiten]
- blocking operations when function call returns when operation has been locally completed (irregardless of success of if data has been sent out etc.)
- non-blocking when function call returns immediately (specified by capital
Iin function name, e.g.MPI_Irecv)
Specifying data[Bearbeiten | Quelltext bearbeiten]
bufferspecifies starting adresscountspecifies number of elementsdatatypespecifies MPI type- e.g.
MPI_(CHAR|INT|LONG|FLOAT|DOUBLE)
- e.g.
One-sided communication[Bearbeiten | Quelltext bearbeiten]
- one process alone initiates communication
- also specifies actions on both ends
- involved processes are called origin and target
Collective communication[Bearbeiten | Quelltext bearbeiten]
If some process calls a collective operation C on a communicator, then all other processes in the communicator must also eventually call C and no other collective before C.
| Regular | Irregular | |
|---|---|---|
| symmetric, no-data |
MPI_Barrier | |
| Rooted (asymmetric) |
MPI_Bcast MPI_Gather MPI_Scatter MPI_Reduce |
MPI_Gatherv MPI_Scatterv |
| Non-rooted (symmetric) |
MPI_Allgather MPI_Alltoall MPI_Allreduce MPI_Reduce_scatter_block MPI_Scan MPI_Exscan |
MPI_Allgatherv MPI_Alltoallv MPI_Alltoallw MPI_Reduce_scatter |
- symmetric vs. non-symmetric
- all processes have the same role in collective vs. one/some process (root) is special
- regular vs. irregular
- each process contributes or receives the same amount of data vs. different pairs of processes may exchange different amounts of data
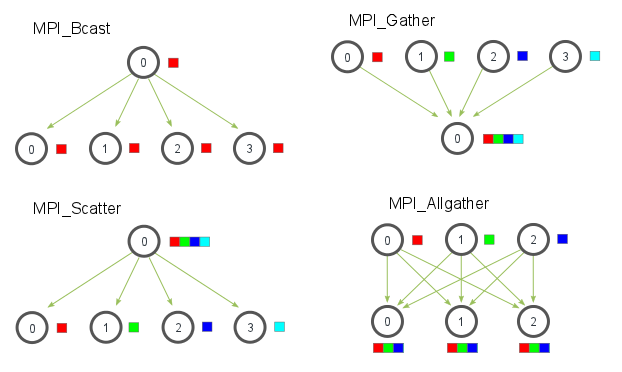
MPI_Barrierblocks until all have reached routineMPI_Bcastto send data fromrootto all nodesMPI_Scatterdistributes data from processrootevenly to all otherMPI_Gathergathers data from all other processes inrootMPI_Allgatherlike Gather but all processes have all dataMPI_Reducereduction of data inrootwith operatorMPI_Op op- operations are assumed to be associative and commutative
MPI_Allreducelike reduce but all processes receive reductionMPI_Reduce_Scatterfirst reduce vector in processes, then scatter vector in segments across processesMPI_Alltoall(could be namedAllscatter) every process scatters their data to all otherMPI_Scanperforms a reduction over a group, where each subsequent process stores the result of the reduction of the current value and the previous values- e.g. Scan with SUM reduction processes with values in brackets: 1(1), 2(2), 3(3), 4(4)
- e.g. Scan with SUM reduction processes with values in brackets: 1(1), 2(2), 3(3), 4(4)
- after Scan: 1(1), 2(3), 3(6), 4(10)
MPI_Exscanlike Scan but value of process is not used in reduction- same example with Exscan: 1(0), 2(1), 3(3), 4(6)