TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 324
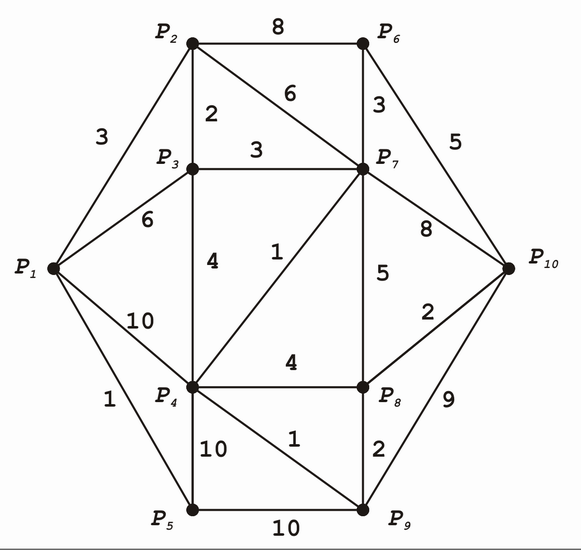
In der folgenden schematisch skizzierten Landkarte sind für eine bestimmte Fracht die Transportkosten zwischen den einzelnen Orten angegeben. Welches ist der billigste Weg vom Ort zum Ort ?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theorie - Algorithmus von Dijkstra[Bearbeiten | Quelltext bearbeiten]
Dijkstra-Kochrezept von Superwayne[Bearbeiten | Quelltext bearbeiten]
Das Ziel des Dijkstra-Algorithmus ist, die kürzeste Distanz von einem Anfangsknoten für einen Endknoten oder alle anderen Knoten zu finden. Am einfachsten ist dafür eine tabellarische Lösung. Für jeden Knoten wird eine Spalte angelegt, sowie eine für den ausgewählten Knoten und den Vorgängerknoten. Mit jeder Zeile "wächst" unser Wissen über den Graph. Eine Zeile ist also eine Iteration, mit der wir mehr wissen über den Graph und seine Zusammensetzung erlangen.
- Anfang: Am Anfang wissen wir natürlich noch nichts über den Graph, wir stehen bildlich gesprochen vor dem Anfangsknoten des Graphen und können nur diesen Anfangsknoten sehen. Deshalb legen wir in der Tabelle die erste Zeile an und setzen für den Anfangsknoten die Distanz 0 und für alle anderen Knoten die Distanz unendlich, da wir diese nicht "sehen" können, also noch kein Wissen über diese haben.
- Auswählen des nächsten Knotens: Nun müssen wir uns entscheiden, welcher Knoten als nächstes ausgewählt werden soll. Dazu wählen wir den Knoten aus der aktuellen Zeile, der den geringsten Wert (Distanz) aufweist und noch nie ausgewählt wurde. Wir wählen diesen Knoten als Nachfolger aus, d.h. wir vermerken dies in der Spalte Ausgewählter Knoten und setzen den aktuellen Knoten als Vorgänger. Gibt es keinen Knoten mehr zum Auswählen oder ist der ausgewählte Knoten unser gesuchter Knoten, so sind wir fertig.
- Bewertung des Knotens: Nachdem wir einen neuen Knoten ausgewählt haben, gehen wir alle noch nicht ausgewählten Knoten Spalte für Spalte durch. Ist der Knoten in der Spalte kein Nachbarknoten, so übernehmen wir die Distanz einfach in die aktuelle Zeile. Ist der Knoten ein Nachbarknoten, so prüfen wir, ob die Distanz über den aktuellen Knoten kleiner ist. Wenn ja, schreiben wir die aktuelle Distanz in die Spalte, wenn nein, übernehmen wir die Distanz aus der vorherigen Zeile. Das machen wir für alle Knoten bzw. alle Spalten. Anschließend gehen wir über zu Auswählen des nächsten Knotens (Punkt 2).
Den kürzesten Weg kann man nun rekonstruieren, in dem man vom letzten ausgewählten Knoten den Vorgänger aus der Tabelle abliest und von diesem Vorgängerknoten wieder den Vorgängerknoten, usw. usf. wodurch man dann den kürzesten Pfad erhält.
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Basierend auf f.thread:37700
Tabellarische Lösung[Bearbeiten | Quelltext bearbeiten]
| Iteration | Auswahl | Vorgänger | ||||||||||
| 0 | 0 | |||||||||||
| 1 | 3 | 6 | 10 | 1 | ||||||||
| 2 | 3 | 6 | 10 | 11 | ||||||||
| 3 | 5 | 11 | 9 | 11 | ||||||||
| 4 | 9 | 8 | ||||||||||
| 5 | 9 | 11 | 13 | 16 | ||||||||
| 6 | 13 | 10 | ||||||||||
| 7 | 12 | 19 | ||||||||||
| 8 | 14 |
Kürzester Weg somit:
Edit: es gibt noch einen zweiten möglichen kürzesten Weg:
tomel: Ich würde eher die zweite Lösung für die korrekte halten, weil im "orangen Buch" auf Seite 69 bei der Beschreibung des Algorithmus in Punkt 2 als Bedingung > und nicht >= angegeben wird. Dh der Vorgänger von P4 bleibt P3, auch wenn er zu denselben Kosten von P7 erreichbar ist, würde ich sagen.
Anmerkung: tomel hat recht, und außerdem ist die Tabelle unvollständig weil zB P6 auf einmal nicht mehr mitgeschrieben wird, in Zeile 7 wäre P6 das Minimum. Und auch dass P10 auf einmal wieder höher wird (von 16 auf 19) macht keinen Sinn. Es wird immer der minimale Weg aufgeschrieben. Diese Schreibweise in der man Lücken lässt wenn sich der Wert nicht gerade geändert hat ist also nicht zu empfehlen, da passieren einem dann solche Fehler wie hier.
Alternative Lösung[Bearbeiten | Quelltext bearbeiten]
Die Tabelle in der obigen Lösung ist meines Erachtens nicht ganz richtig, da nicht immer der absolut kürzeste, dem System zum Zeitpunkt bekannte, Weg gewählt wird (der auch für die Lösung gesehen sein kann). Ich habe deshalb die Tabelle noch einmal aufgebaut. Das Ergebnis ist zwar das gleiche, aber man kann dann den Algorithmus vielleicht leichter nachvollziehen. Dieses Beispiel ist vor allem deshalb interessant, da es Spezialfälle enthält.
| Ausgewählter Knoten | Vorgängerknoten | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | - | |
| – | 3 | 6 | 10 | 1 | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| – | 3 | 6 | 10 | – | ∞ | ∞ | ∞ | 11 | ∞ | ||
| – | – | 5 | 10 | – | 11 | ∞ | ∞ | 11 | ∞ | ||
| – | – | – | 9 | – | 11 | 8 | ∞ | 11 | ∞ | ||
| – | – | – | 9 | – | 11 | – | 13 | 11 | 16 | ||
| – | – | – | – | – | 11 | – | 13 | 10 | 16 | ||
| – | – | – | – | – | 11 | – | 12 | – | 16 | ||
| – | – | – | – | – | – | – | 12 | – | 16 | ||
| – | – | – | – | – | – | – | – | – | 14 |
Rückwärts ausgelesen ist die Lösung demnach bzw. .
-- Superwayne 20:30, 27. Nov. 2014 (CET)
Anmerkung: Dies ist meiner Meinung nach nicht korrekt. Wenn ich für einen Punkt einen Wert w bekomme und im Laufe des Algorithmus den gleichen Wert w zum selben Punkt ausgehend von einem anderen Vorgänger bekomme, so wird immer nur der erste kürzeste Weg in Betracht gezogen und nicht beide oder der letzte.