TU Wien:Mathematik 1 UE (diverse)/Theorie WS05/06.12.2005 Graphentheorie
Beispiele[Bearbeiten | Quelltext bearbeiten]
Königsberger Brückenproblem[Bearbeiten | Quelltext bearbeiten]
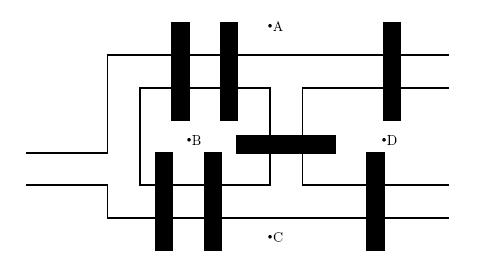
Kann man einen Spaziergang durch die Stadt machen und dabei ?üer jede Br?üke gehen, aber ?über jede nur einmal? Und nach dem Spaziergang möhte man wieder nach Hause, d.h. zum Ausgangspunkt zur?ückkehren. (http://de.wikipedia.org/wiki/K%C3%B6nigsberger_Br%C3%BCckenproblem, 1736 v. leonhard EULER aufgestellt).
Haus vom Nikolaus[Bearbeiten | Quelltext bearbeiten]
Entscheide, ob man das Bild zeichnen kann, ohne den Stift abzusetzen und ohne eine Linie doppelt zu ziehen! ( http://de.wikipedia.org/wiki/Haus_vom_Nikolaus )
Reisepläne[Bearbeiten | Quelltext bearbeiten]
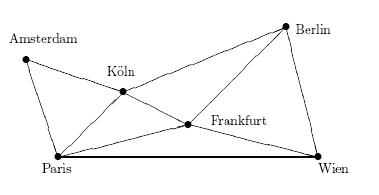
St?ätetour mit Euro - Ticket: Start in Berlin, Fahrt durch alle im Plan eingezeichneten St?äte, durch jede nur einmal, und Fahrt soll in Berlin enden (jede Stadt einmal besuchen, es muss nicht jede Strecke abgefahren werden; Hamilton Graph/Kreis). Dies muss keine "eulersche Tour" sein.
Problem des Handlungsreisenden[Bearbeiten | Quelltext bearbeiten]
Das Problem ist als Problem des Handlungsreisenden (Traveling Salesman Problem, (TSP)) bekannt: Ein Gesch?ätsmann muss in mehreren Orten Kunden betreuen und danach in sein B?üro zur?ückkehren. Er m?öchte seine Fahrtroute so planen, dass er durch jeden Ort nur einmal kommt und dass ausserdem die zurückgelegte Strecke m?oglichst kurz wird (kürzester hamiltonscher Kreis\).
Chinese Postman Problem[Bearbeiten | Quelltext bearbeiten]
Suche geschlossenen Weg durch Zufallsgebiet, möglichst kurz, nur an Strassenecken sind Briefkästen
aufspannende Bäume[Bearbeiten | Quelltext bearbeiten]
In einer ländlichen Gegend sollen zwischen mehreren Ortschaften Strassen neu gebaut werden. Es soll jeder Ort von jedem anderen Ort auf einer der Strassen erreicht werden können.
minimal aufspannender Baum[Bearbeiten | Quelltext bearbeiten]
Wenn in vorhergehendem Punkt noch die gesamten Baukosten möglichst niedrig sein sollen, sucht man einen minimalen aufspannenden Baum.
kürzeste Wege[Bearbeiten | Quelltext bearbeiten]
Wir haben einen Strassenplan vor uns und befinden uns an einer Stelle u. Wir möchten von u in m?öglichst kurzer Zeit nach v kommen.
Labyrinth-Problem[Bearbeiten | Quelltext bearbeiten]
Labyrinth an einer Stelle betreten, alle Wege im Labyrinth erkunde und wieder herausfinden.
Netzwerke[Bearbeiten | Quelltext bearbeiten]
Routingtabellen im Internet z.B. (Distance Vector oder Bellman/Ford-Algorithmus sowie den Link State oder Dijkstra-Algorithmus).
Maximaler Durchfluss in Netzen - Algorthmus von Ford-Fulkerson.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Sollten wir zu den gestellten Problemen Lösungen finden k?onnen, so sind wir jeweils auch an einem Verfahren interessiert, die jeweilige Lösung zu finden, also an einem Algorithmus.
Grundbegriffe der Graphentheorie[Bearbeiten | Quelltext bearbeiten]
Bestandteile eines Graphen[Bearbeiten | Quelltext bearbeiten]
Ein Graph besteht aus Ecken (Knoten) und Kanten, wobei eine Kante genau zwei Ecken verbindet. Je zwei Ecken können also durch keine, eine oder mehr als eine Kante verbunden sein.
Notation: G(E;K); E: Knotenmenge; K: Kantenmenge.
Vollständige Graphen[Bearbeiten | Quelltext bearbeiten]
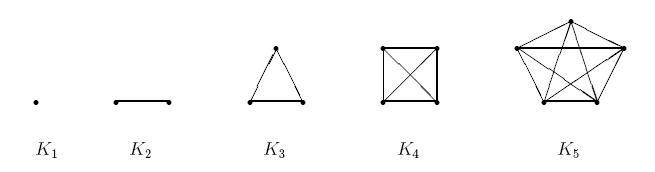
Ein Graph heisst vollständig, wenn jede Ecke mit jeder anderen Ecke durch genau eine Kante verbunden ist.
bezeichnet den vollständigen Graphen mit n Ecken.
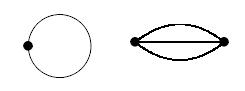
Schlingen und Mehrfachkanten[Bearbeiten | Quelltext bearbeiten]
Schlingen und Mehrfachkanten sind grundsätzlich zugelassen, aber Graphen ohne solche werden einfache Graphen genant und um diese geht es hier zumeist.
verschiedene Diagramme für einen Graphen[Bearbeiten | Quelltext bearbeiten]
verschiedene Diagramme für denselben Graphen
Weitere Begriffe[Bearbeiten | Quelltext bearbeiten]
Gittergraphen ()
m * n Knoten wie in einem Gitter mit m Zeilen und n Spalten verbunden
Kreis ()
n Knoten, die zyklisch miteinander verbunden sind
Weg/Pfad ()
n + 1 Knoten und n Kanten, die aufeinanderfolgende Knoten miteinander verbinden.
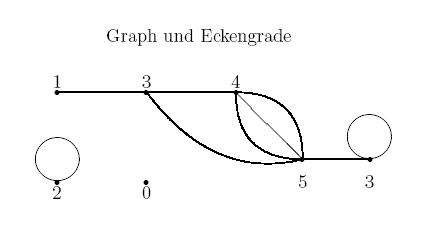
Eckengrade (Knotengrade)[Bearbeiten | Quelltext bearbeiten]
Die Anzahl der Kanten, die von einer Ecke ausgehen, bezeichnet man als Grad der Ecke, in Notation deg(e).
- deg(e) = 0: isolierte Ecke
- deg(e) = 1: Blatt
Beispiele:
- : deg(e) = n + 1 für alle e
- : deg(e) = 2 für alle e
Handschlaglemma[Bearbeiten | Quelltext bearbeiten]
denn jede Kante liefert genau zweimal einen Beitrag zu der Summe der Grade.
Daraus ergibt sich als Schlussfolgerung (auch Korollar genannt): In endlichen Graphen ist die Anzahl der Knoten mit ungeradem Grad gerade. (Sonst wäre die Summe der Grade ungerade, was nach obiger Formel nicht geht.)
Zusammenhängende Graphen[Bearbeiten | Quelltext bearbeiten]
sei ein Graph; ein Graph G(F,L)' mit und Untergraph, Teilgraph, Subgraph.
Im Fall E = F heißt G(F,L) aufspannender Untergraph (spanning subgraph).
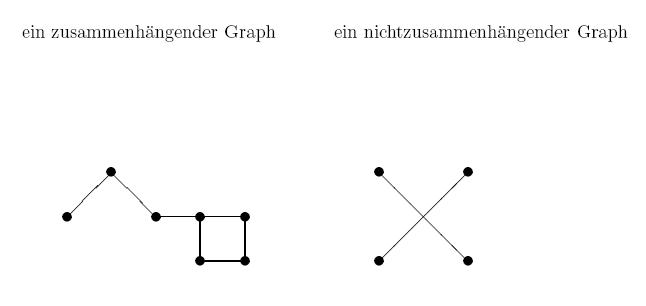
heisst zusammenhängend genau dann, wenn je zwei Knoten durch einen Weg verbunden werden können (ein Weg von e nach f existiert).
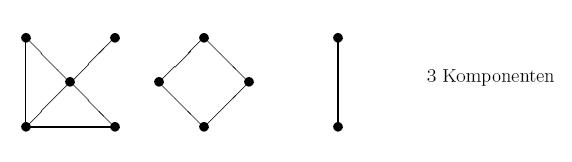
Größtezusammenh?angende Teilgraphen von heißen Komponenten. (Wenige Kanten sind ein Hinweis auf viele Komponenten).
Jeder Graph enthältt mindestens viele Komponenten.
Für jeden zusammenh?angenden Graphen gilt
Isomorphie[Bearbeiten | Quelltext bearbeiten]
Zwei Graphen und heißen isomorph, wenn es eine 1-1-Abbildung gibt mit mit e durch Kante verbunden mit f mit durch Kante verbunden mit .
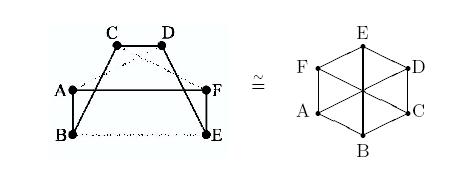
Zwei Graphen sind genau dann isomorph, wenn der eine Graph aus dem anderen Graphen durch Umbenennung der Knoten hervorgeht.
Beispiele[Bearbeiten | Quelltext bearbeiten]
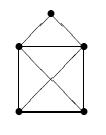
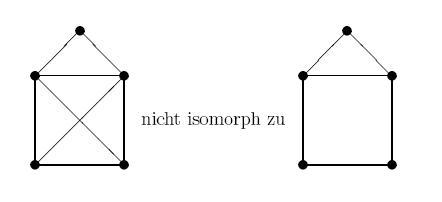
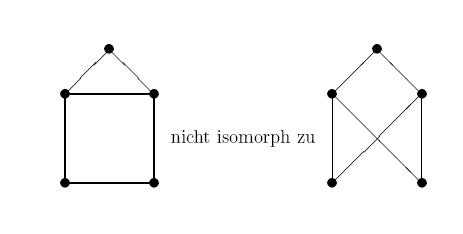
Beide Graphen haben 5 Ecken und 6 Kanten, davon 3 Ecken mit Grad 2, 2 Ecken mit Grad 3. Im linken Graphen sind die Ecken mit Grad 3 verbunden, rechts hingegen nicht.
Hamiltonsche Kreise und Eulersche Graphen[Bearbeiten | Quelltext bearbeiten]
Zum Problem der Rundreise[Bearbeiten | Quelltext bearbeiten]
Sir William Rowan Hamilton (1805 - 1865) erfand 1859 das Spiel "Around the world".
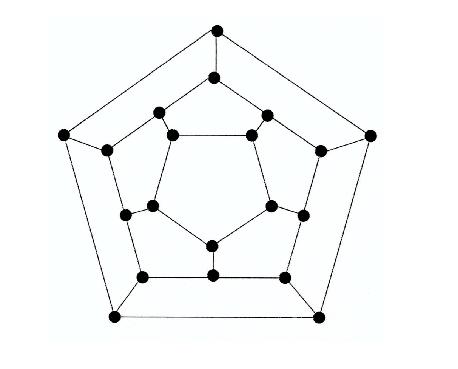
Die Punkte eines Dodekaeders (regelm. Zwölfflächner) stellen Städte dar. Die Aufgabe besteht darin, entlang der Kanten des Dodekaeders eine Rundreise zu unternehmen, bei der man jede Stadt genau einmal besucht.
Seit Platon ist bekannt, dass es nur fünf regul?are konvexe Polyeder gibt. (Alle seine Obeflächen bestehen aus denselben regelmäßigen Vielecken und in jeder Ecke stossen gleich viele dieser Vielecke zusammen.)
- Tetraeder (4 Dreiecke) (tetra)
- Hexaeder (6 Quadrate) (hexa)
- Oktaeder (8 Dreiecke) (okta)
- Pentagon: Dodekaeder (12 Fünffecke) (pentagon)(gr. dodeka = 12)
- Ikosaeder (20 Dreiecke) (gr. eikosa = 20)
Hamiltonscher Kreis[Bearbeiten | Quelltext bearbeiten]
Es sei G(E,K) ein endlicher Graph. Ein Weg, der jeden Knoten von G genau einmal enthält, heisst hamiltonscher Weg; ein Kreis, der jeden Knoten von G genau einmal enthält, heisst hamiltonscher Kreis oder Hamilton-kreis.
G(E,K) heisst hamiltonsch genau dann, wenn G einen hamiltonschen Kreis enthält.
Satz von Dirac[Bearbeiten | Quelltext bearbeiten]
Erfüllt ein Graph G(E,K) die Bedingung
für alle , so enthält er einen Hamiltonkreis.
Erfüllt ein Graph für jeden Knoten, so ist er hamiltonsch (Dirac).
Hamiltonscher Kreis eines Beispielgraphen:
Entfernt man eine Ecke und mit ihr alle Kanten, die zu dieser Ecke führen, so bleibt der Graph zusammenhängend. Daraus folgt:
Ist es möglich, in einem Graphen eine Ecke zu entfernen und mit ihr alle Kanten, die in ihr enden, und zerfällt der Graph dann in zwei oder mehr Teile, die nicht mehr zusammenhängend sind, so ist der Graph nicht hamiltonsch.
ist hamiltonsch und wir zählen die hamiltonschen Kreise:
- enthält einen hamiltonschen Kreis.
- enthält 3 hamiltonsche Kreise.
enthält hamiltonsche Kreise
Weitere Beispiele[Bearbeiten | Quelltext bearbeiten]
- Sitzordnungen (Optimale Platzierungen)
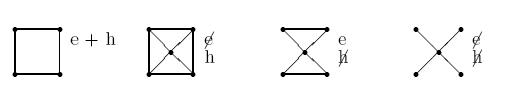
Eulersche Graphen[Bearbeiten | Quelltext bearbeiten]
Eine Eulertour in einem Graphen ist ein Weg, der jede Kante des Graphen genau einmal enthält und dessen Anfangs- und Endknoten identisch sind. Enthält der Graph eine Eulertour, so nennt man ihn eulersch (eulerscher Kreis).
Beispiel: Nikolaus mit Keller
Alle Ecken haben ungeraden Grad. Jede Ecke müsste Anfangs- oder Endpunkt des Spaziergangs sein!
Vor einer Charakterisierung eulerscher Graphen ein Vergleich zu hamiltonsch:
- eulersch: jede Kante genau einmal
- hamiltonsch: jede Ecke genau einmal
Ein zusammenhängender Graph G(E,K) ist genau dann eulersch, wenn der Grad aller Knoten gerade ist.
Bäume und Wälder[Bearbeiten | Quelltext bearbeiten]
Ein Graph heisst ein Baum, falls er zusammenhängend ist und keine Kreise enthält. Ein Graph, dessen Komponenten jeweils Bäume sind, heisst ein Wald.
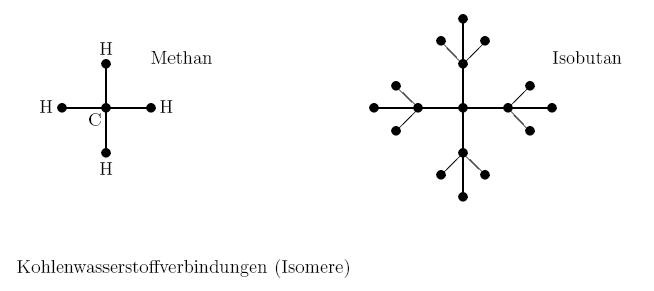
Beispiele für Bäume[Bearbeiten | Quelltext bearbeiten]
Cayley beschäftigte sich Ende des 19. Jahrhunderts mit der Frage, wie viele verschiedene Isomere einer bestimmten Zusammensetzung existieren.
Bäume mit höchstens 5 Ecken:
Weitere Bäume sind:
Aufspannende Bäume[Bearbeiten | Quelltext bearbeiten]
G(E,K) sei ein zusammenhängender Graph. Ein Teilgraph T der ein Baum der Ordnung n = |E| ist, heissr ein aufspannender Baum (manchmal Gerüst).
Jeder zusammenhängende Graph G besitzt aufspannende B?aume.
Denn entweder ist G bereits ein Baum, dann sind wir fertig, oder G besitzt einen Kreis C. Entfernen wir aus C eine Kante k so ist
immer noch zusammenhängend. Entweder ist ein aufspannender Baum oder besitzt wieder einen Kreis, : Wir entfernen eine Kante aus u.s.w.
Nach endlich vielen Schritten erhalten wir einen aufspannenden Baum. (Anderer Weg: wähle aus G eine beliebige Kante aus, dann eine zweite, eine dritte usw. und achte jeweils darauf, dass kein Kreis entsteht. Wenn alle Ecken an einer dieser Kanten hängen, ist der aufspannende Baum fertig.)
In der Anwendung bei Versorgungssystemen (Wasser, Strom, Telefon) benutzt man keine Bäume, denn bei defekten Leitungen muss das System noch mindestens ein aufspannender Baum sein!
Folgende Aussagen sind äquivalent:
- G(E,K) ist ein Baum.
- Je zwei Ecken in G sind durch genau einen Weg verbunden.
- G ist zusammenh?angend und |E| - 1 = |K|.
Die Anzahl der aufspannenden Bäume aus ist:
Aus n Ecken kann man also Bäume herstelleb.
Minimal aufspannede Bäume[Bearbeiten | Quelltext bearbeiten]
Kommunikationsnetz: Schaltelemente / Ecken, Verbindungen / Kanten.
Kosten der Verbindung zwischen u und v : w(uv)
Aufgabe: Schaltplan konstruieren, so dass jedes Element mit jedem anderen kommunizieren kann und die Gesamtkosten minimal sind!
Gewichteter Graph G(E,K); w:.
Gesucht ist ein aufspannender Baum T mit mininalem Gewicht
Naiv: Wähle Kante von minimalem Gewicht. Hat man schon j Kanten bestimmt, so wähle man als n?ächstes eine Kante minimalen Gewichts, so dass kein Kreis entsteht. Nach n - 1 Schritten (n = |E|) ist ein Baum konstruiert.
Ist dieser Baum optimal? Antwort: ja. Der entsprechende Algorithmus ist der ...
Algorithmus von Kruskal[Bearbeiten | Quelltext bearbeiten]
(http://de.wikipedia.org/wiki/Algorithmus_von_Kruskal)
Der Algorithmus von Kruskal ist ein Algorithmus der Graphentheorie mit dessen Hilfe man Minimal spannender Baum|minimale Spannbäume in zusammenhängenden, ungerichteten, kantengewichteten Graphen berechnen kann. Der Algorithmus wurde von Joseph Kruskal geschrieben und erschien erstmals 1956 in der Zeitschrift „Proceedings of the American Mathematical Society“.
Algorithmus[Bearbeiten | Quelltext bearbeiten]
Die Grundidee ist, die Kanten in Reihenfolge aufsteigender Kantengewichte zu durchlaufen und jede Kante zur Lösung hinzuzufügen, die mit allen zuvor gewählten Kanten keinen Kreis bildet. Es werden somit sukzessiv sogenannte Komponenten zum minimalen Spannbaum verbunden.
Input[Bearbeiten | Quelltext bearbeiten]
Als Eingabe dient ein zusammenhängender kantenbewerteter Graph . bezeichnet die Menge der Ecken (vertices), die Menge der Kanten (edges). Die Gewichtsfunktion ordnet jeder Kante einen Zahlenwert zu.
Output[Bearbeiten | Quelltext bearbeiten]
Der Algorithmus liefert einen minimalen Spannbaum mit .
Algorithmus[Bearbeiten | Quelltext bearbeiten]
Der Algorithmus von Kruskal arbeitet nicht deterministisch, d.h. er liefert unter Umständen beim wiederholten Ausführen unterschiedliche Ergebnisse. Diese Ergebnisse sind allesamt minimale Spannbäume von und damit gleichwertige Lösungen.
- Sortiere die Kanten von aufsteigend nach ihrer Bewertung.
- Setze und .
- Solange , wobei die Anzahl von Komponenten ist, wähle in eine Kante mit kleinster Bewertung. Entferne aus .
- Wenn keinen Kreis enthält, füge zu hinzu.
- Dann ist ein minimaler Spannbaum von .
Derselbe Algorithmus lässt sich analog für einen maximalen Spannbaum anwenden.
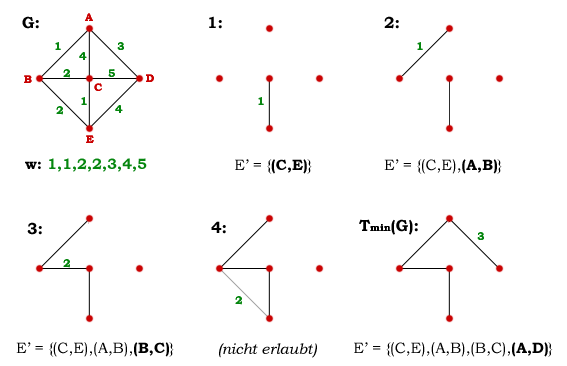
Beispiel[Bearbeiten | Quelltext bearbeiten]
Kürzeste Wege (Dijkstra-Algorithmus)[Bearbeiten | Quelltext bearbeiten]
Finde in einem bewerteten Graph zwischen zwei vorgegebenen Ecken einen Verbindungsweg mit der kleinsten Bewertung.
Beispiel[Bearbeiten | Quelltext bearbeiten]
( http://www.mcgods.de/fun/1904/node8.html )
Im Folgenden wird mit Hilfe des ersten Graphen gezeigt, wie der Algorithmus von Dijkstra funktioniert. Dazu werden vom Knoten 1 die kürzesten Wege zu allen anderen Knoten berechnet. D
Die Grundidee ist, ausgehend vom Startknoten einen Teilgraphen wachsen zu lassen, der erst nur wenige Knoten, am Ende alle Knoten des Ausgangsgraphen umfasst. Die Knoten lassen sich zu jedem Zeitpunkt in drei Klassen einteilen:
- Grüne Knoten sind bereits abschließend besucht worden, mithin also bzgl. ihrer Entfernung zum Ausgangsknoten bereits bestimmt. Sie befinden sich im Inneren des Teilgraphen.
- Rote Knoten befinden sich am Rand des Teilgraphen. Sie sind also mit mindestens einer Kante mit einem Knoten verbunden, der nicht grün ist.
- Weiße Knoten sind noch nicht in den Teilgraphen aufgenommen worden, also Knoten des Ausgangsgraphen.
Genauso lassen sich drei Arten von Kanten unterscheiden:
- Grüne Kanten sind Kanten, die auf einem kürzesten Weg im Teilgraphen vorkommen.
- Rote Kanten sind bereits in den Teilgraphen aufgenommen worden. Sie gehören im Betrachtungszeitpunkt nicht zu einem kürzesten Weg.
- Weiße Kanten sind die noch nicht untersuchten Kanten des Ausgangsgraphen.
Lesehinweis: Weil die Darstellung der Farben im Schwarzdruck Probleme bereitet, wurden verschiedene Strichstärken verwendet: grün ist dunkelgrau-fett, rot ist "dunkelgrau-dünn" und weiß ist "schwarz-getrichelt".
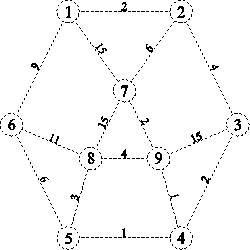
Es erleichtert das Verstehen des Algorithmus, sich die Funktionsweise an einem Beispiel klarzumachen. Sei der Graph in obenstehende Abbildung der zu untersuchende Graph und sei 1 der Startknoten.
1. Zu Beginn wird der Graph initialisiert: Alle Knoten sind weiß, alle Kanten ebenso. Der Startknoten wird rot gefärbt, befindet sich also alleinig auf dem Rand des Teilgraphen:

2. Dann wird der Startknoten grün gefärbt. Seine weißen Nachbarn 2, 6 und 7 werden rot gefärbt. Sie befinden sich jetzt am Rand des untersuchten Teilgraphen. 1 ist als einziger Knoten im Innern. Die zu 2, 6 und 7 führenden Kanten werden grün, da es die kürzesten Wege zu ihnen sind:
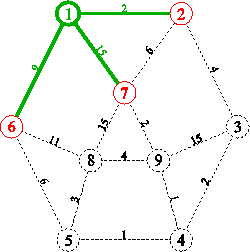
3. Der Knoten 2 ist nun der rote Knoten mit minimalem Abstand zu 1. Er wird grün gefärbt. Gleichzeitig werden seine Nachbarn 3 und 7 rot. Die Kante zu 3 wird grün, da sie auf dem bislang kürzesten Weg zu 3 liegt. Die Kante zu 7 wird ebenfalls grün, da der neue Weg über 2 eine Länge von 2 + 6 = 8 aufweist, die bisherige Länge jedoch 15 war. Als Konsequenz dieser Grünfärbung mit neuer kürzester Länge wird die Kante von 1 zu 7 rot gefärbt, ist also nicht mehr Bestandteil eines kürzesten Weges.
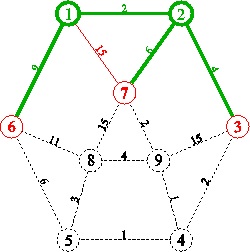
4. Nun ist der Knoten 3 mit einer Entfernung von 6 der Knoten mit der minimalen Entfernung zu 1. Dieser wird grün gefärbt, wandert also ins innere des Teilgraphen. Dabei werden 4 und 9 rot gefärbt, liegen also am Rand. Die Kanten zu 4 und 9 erhalten grüne Färbung.
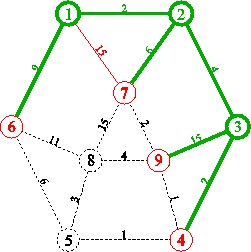
5. Minimal sind 4 und 7, Entfernung jeweils 8. Es wird zufällig 4 gewählt. Damit wird 4 grün und 5 und 9 rot. Da 9 erneut erreicht wird, wird die bisherige Entfernung 21 mit der neuen Entfernung über 4, also mit 9 verglichen. Da die neue kürzer ist, wird die Kante 4 nach 9 grün, die Kante 3 nach 9 rot.
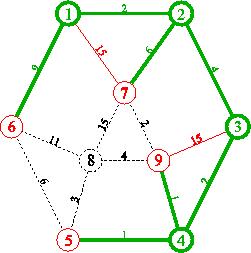
6. Minimal ist jetzt 7, wiederum Entfernung 8. 7 wird also grün, 8 und 9 rot. Die Kante 7 nach 8 wird rot, die Kante 7 nach 9 ebenso, da 9 zwar erneut erreicht wird, die bisherige Entfernung (9) jedoch kürzer als die neue (10) ist.

7. Minimal sind 5, 6 und 9 mit jeweils Entfernung 9. Zufällig wird 5 gewählt, also 5 grün. Neu rot zu färbende Knoten treten nicht mehr auf. Die benachbarten roten Knoten 6 und 8 sind jedoch hinsichtlich der alten und neuen Entfernung zu untersuchen, ob eine Kante umgefärbt werden muss.

8. Weiter mit 6.
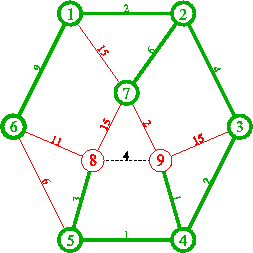
9. Weiter mit 9.

10. Schließlich verbleibt nur noch Knoten 8. Dieser wird abschließend grün gefärbt. Da keine roten Nachbarknoten mehr zu betrachten sind, ist nichts weiteres zu tun.

Die kürzesten Entfernungen von Knoten 1 zu allen anderen Knoten lassen sich leicht aus dem Schlussgraphen ablesen.