TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 126
Sei .
Ist R eine Halbordnung auf ?
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Halbordnung[Bearbeiten | Quelltext bearbeiten]
Eine binäre Relation R auf einer Menge A heißt Halbordnung oder partielle Ordnung, wenn folgende drei Eigenschaften erfüllt sind:
- Reflexivität: ,
- Antisymmetrie: ,
- Transitivität: .
Damit die Relation R eine Halbordnung ist, muß sie die Eigenschaften Reflexivität, Antisymmetrie und Transitivität erfüllen.
Reflexivität: ?
reflexiv.
Antisymmetrie: ?
Aus folgt . Diese Äquivalenz ist aber nicht nur erfüllt, wenn , sondern aufgrund der Absolutbeträge auch wenn , daher ist R nicht antisymmetrisch.
Von Axel:
Ich habe die Antisymmetrie ein bisserl anders gemacht, der Grund: Wenn ich das Widerlegen von "Aus |m|<=|n| und |n|<=|m| folgt |m|=|n|" als Beweisgrundlage hernehme, dann wird der Panholzer fragen woher ich wissen will, dass "Aus |m|<=|n| und |n|<=|m| folgt |m|=|n|" und "mRn und nRm impliziert n=m" Äquivalent sind ;-)
Wenn man das gleich "von hinten rum" macht geht es imho einfacher:
Beweise/Wiederlege die Annahme: Aus mRn und nRm folgt m=n fuer alle m,n Element Z.
Sei m Element Z und m groesser 0 und n = -m. Dann ist wegen |m|<=|-m| mRn gegeben, und wegen |-m|<=|m| nRm geben, aber m ungleich n, also die Annahme wiederlegt.
Von Jens: Aus folgt aufgrund der Antisymmetrie der Halbordnung , daß . So ist die Definition der Kleiner-gleich-Relation, das mußt Du nicht extra beweisen.
Transitivität: ?
Daraus folgt, daß R transitiv ist.
Da R nur die Eigenschaften Reflexivität und Transitivität erfüllt, nicht aber die Antisymmetrie, ist R keine Halbordnung auf .
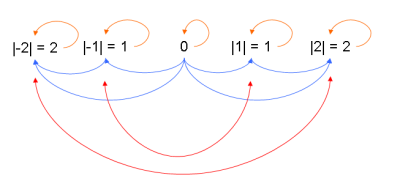
Graphische Ergänzung[Bearbeiten | Quelltext bearbeiten]
Orangene Linien zeigen die Reflexivität, da und
Blaue Linien zeigen Transitivität, da und
Rote Linien widerlegen die Antisymmetrie, da und