TU Wien:Algebra und Diskrete Mathematik VO (Karigl)/Prüfung 2013-05-08

siehe auch Thread im Informatikforum

Aufgabe 1

Man bestimme die allgemeine Lösung der Differenzengleichung $x_{n+1}=\frac{2}{3}{x}_n+1$ (für $n\ge 0$) und die partikuläre Lösung, die der Anfangsbedingung $x_0=7$ genügt.

Aufgabe 2

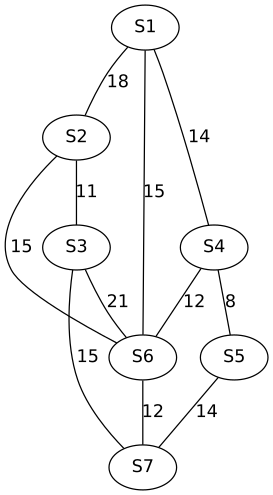
Sieben Rechner-Knoten sollen über ein Hochgeschwindigkeits-Datennetz miteinander verbunden werden. Die in Betracht kommenden Leitungsführungen und deren Kosten sind in nachstehendem bewertetem Graphen angegeben. Man bestimme alle kostenminimalen Datennetze, an die sämtliche Knoten angeschlossen sind, sowie deren Gesamtkosten.

Aufgabe 3

Gegeben sei die Matrix

$A=\left(\begin{array}{ccc}13& 0& -12\\ 12& 1& -12\\ 16& 0& -15\end{array}\right)$

Man zeige, dass $\lambda =1$ ein Eigenwert von $A$ mit der Vielfachheit 2 ist, und berechne alle zugehörigen Eigenvektoren.

Aufgabe 4

Lineare Abhängigkeit in Vektorräumen:

• Man erkläre die Begriffe "linear abhängig" bzw. "linear unabhängig" für Vektoren eines Vektorraums $V$ über dem Körper $ℝ$.
• Ferner gebe man je ein Beispiel mit drei linear abhängigen bzw. linear unabhängigen Vektoren im ${ℝ}^3$.
• Was versteht man unter einer Basis eines Vektorraums $V$?
• Schließlich gebe man zwei verschiedene Basen für den Vektorraum $P_2(ℝ)$ aller Polynome $a+bx+c{x}^2$ vom Grad kleiner gleich 2 mit Koeffizienten $a,b,c\in ℝ$ an.

Aufgabe 5

Es sei $\text{R}$ jene binäre Relation auf $\mathbb{Z}$, welche durch $a\text{R}b\iff a\equiv bmod2013$ definiert ist. Man beantworte die folgenden Fragen (bitte ankreuzen, es können keine, genau eine oder auch mehrere Antworten zutreffend sein).

• Für die Relation $\text{R}$ gilt:
  • $\text{R}\subseteq \mathbb{Z}$
  • $\text{R}\subseteq {\mathbb{Z}}^2$
  • $\text{R}\subseteq \mathbb{Z}\times \mathbb{Z}$
• Die Relation $\text{R}$ ist:
  • symmetisch
  • antisymmetrisch
• Ist die Relation $\text{R}$ reflexiv?
  • ja
  • nein
• Ist $\text{R}$ eine Äquivalenzrelation?
  • ja
  • nein
• Ist $\text{R}$ eine Halbordnungsrelation?
  • ja
  • nein
• Induziert die Relation $\text{R}$ eine Partition auf der Menge $\mathbb{Z}$?
  • ja
  • nein
• Kann $\text{R}$ durch ein Hasse-Diagramm dargestellt werden?
  • ja
  • nein
• Die Relation $\text{R}$ ist:
  • injektiv
  • surjektiv
  • bijektiv